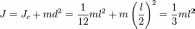- •Связи и их реакции.
- •Геометрический способ нахождения равнодействующей плоской системы сходящихся сил
- •Аналитический способ нахождения равнодействующей плоской системы сходящихся сил
- •Пара сил. Момент пары сил
- •Момент силы относительно точки
- •Плоская система произвольно-расположенных сил. Условия равновесия
- •Формы уравнений равновесия плоской системы произвольно расположенных сил
- •Пространственная система сходящихся сил
- •Пространственная система произвольно расположенных сил
- •11.Момент силы относительной оси
- •12.Условия Пространственной системы произвольно расположенных сил
- •13.Центр тяжести. Способы определение центра тяжести. Координаты центра тяжести плоского тела и составленных сечений.
- •14.Скорость точки
- •15.Ускорение точки
- •16.Поступательные движения твердого тела
- •17.Вращательное движение твердого. Частные Случаи вращательного движения твердого тела.
- •18.Угловая скорость.19Угловое ускорение
- •20.Основные формулы равномерного и равномерно-переменного движения
- •Графики прямолинейного равномерного движения.
- •21.Сложные движения твердого тела. Плоскопараллельное движение. Мгновенные центра скоростей.
- •2.2. Описание движений твердого тела
- •2.3 Плоскопараллельное движение твердого тела
- •23.Аксиомы динамики
- •24.Методы кинематики
- •25.Работа при постоянной силе при прямолинейном движении, при вращательном движении. Работы силы тяжести
- •4.3 Работа постоянной силы на прямолинейном перемещении
- •26.Мощность.Кпд. А. Трение скольжение b.Трение Качение
- •27.Общие теоремы динамик
- •28.Основные уравнения динамики для вращательного движения твердого тела
- •29.Основные гипотезы и допущения сопротивлении материалов
- •30.Методи сечения
- •31.Внутненние силы в поперечном сечении
- •32.Напряжение полное, нормальное, касательное.
- •33.Растяжение, сжатие. Продольные силы и их эпюры.
- •Продольное сжатие
- •34.Нормальные напряжения и их эпюры
- •35.Условия прочности при растяжении, сжатии. Допускаемые напряжения.
- •36.Закон Гука при растяжении, сжатии.
- •37.Срез и смятие. Основные допущения на срез и смятия.
- •38.Расчет на срез и смятие
- •39.Кручение. Деформация при кручении
- •40.Правила построение эпюр крутящий момент.
- •41.Напряжение при кручении
- •42.Расчет на прочность и сжатие при кручении
- •43.Осевые моменты энергии. Моменты инерции некоторых Простейших сечений
- •44.Полярный момент инерции. Полярный момент инерции для круга, для кольца.
- •45.Изгиб. Основные понятия
- •46.Поперечные силы. Правила построение эпюр поперечных сил.
- •47.Изгибающие моменты. Правила построение эпюр изгибающий момент.
- •3.5. Построение эпюр изгибающих моментов и поперечных сил.
- •48.Диффиринциальная зависимость интенсивностью распространению нагрузки, поперечной силой и изгибающим моментом.
- •49. Расчет на прочность при изгибе.
- •50.Гипотизы прочности при изгибе.
- •51.Критическая сила для сжатие стержней
- •2.6.1. Критическая сила
- •52.Условия устойчивости для сжатых стержней
- •53.Основные критерии работоспособности и расчете деталей машин.
- •54.Основные кинематические и силовые соотношения в механических передачах.
- •55.Фрикционне передачи. Их достоинство и недостатки. Область применение, классификации.
- •Раздел 13. Фрикционные передачи.
- •Передача с катками клинчатой формы
- •56.Зубчатые передачи. Их достоинство и недостатки. Область применение, классификации.
- •57.Виды разрушений зубьев
- •58.Материялы зубчатых колес
- •4.3.1 Материалы, применяемые для изготовления зубчатых колес
- •59.Сылы, действующие в зацеплении зубчатых передач
- •1.6.1. Основы теории зацепления
- •60.Расчет прямозубых цилиндрических колес на усталость.
- •61.Передача винт-гайка. Достоинство и недостатки. Область применения.
- •5.1 Назначение и область применения передачи винт-гайка
- •5.2 Достоинства передачи винт-гайка
- •5.3 Недостатки передачи винт-гайка
- •62.Червячная передача. Достоинство и недостатки. Область применения.
- •63.Ременная передача. Достоинство и недостатки. Область применения, классификация.
- •64.Силы действующих в ременных передачах. Скольжение ремня
- •§ 17.4. Скольжение ремня. Передаточное число
- •65.Цепные передачи. Достоинства и недостатки. Область применения.
- •8.1 Назначение и область применения цепных передач
- •8.2 Достоинства цепных передач
- •8.3 Недостатки цепных передач
- •66.Силы действующие в цепных передачах.
- •67.Оси и валы. Расчет волов и осей на прочность. Валы и оси. Основы расчета на прочность, жесткость и выносливость
- •68.Подшипники скольжения. Их достоинства и недостатки. Область применения.
- •69.Подшипники качения. Их достоинства и недостатки. Область применения.
- •70.Класификация подшипников качения
- •71.Классификация муфт
- •72.Неразъемные соединения. Общие сведения. Общие сведения сварных соединений
- •Преимущества сварного соединения
- •Недостатки сварного соединения
- •Виды сварных соединений
- •Геометрия сварного шва
- •Критерии работоспособности сварных соединений
- •73.Расчет на прочность сварных соединений.
- •74.Резьбовые соединения
41.Напряжение при кручении
Вращающийся
стержень, работающий на кручение
называют 0%92%D0%B0%D0%BB_(%D1%82%D0%B5%D1%85%D0%BD%D0%B8%D0%BA%D0%B0)"валом.
Стержень, используемый как упругий
элемент, который работает на скручивание,
называется 0%A2%D0%BE%D1%80%D1%81%D0%B8%D0%BE%D0%BD"торсионом.
Касательные напряжения  ,
возникающие в условиях кручения,
определяются по формуле:
,
возникающие в условиях кручения,
определяются по формуле:
 ,
,
где r — расстояние от оси кручения.
Очевидно,
что касательные напряжения достигают
наибольшего значения на поверхности
вала при  и
при максимальном крутящем моменте
и
при максимальном крутящем моменте 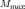 ,
то есть
,
то есть
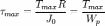 ,
,
где Wp — 0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D1%81%D0%BE%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F&action=edit&redlink=1"полярный момент сопротивления.
Это даёт возможность записать условие прочности при кручении в таком виде:
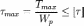 .
.
Используя это условие, можно или по известным силовым факторам, которые создают крутящий момент Т, найти полярный момент сопротивления и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот — зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок.
42.Расчет на прочность и сжатие при кручении
Расчеты на прочность и жесткость при кручении
Условие прочности бруса при кручении заключается в том, что наибольшее касательное напряжение, возникающее в нем, не должно превышать предельно допустимое. При этом расчетная формула на прочность имеет вид:
τmax = Мкр / Wr ≤ [τкр],
где [τкр] - предельное допускаемое напряжение.
При практических расчетах, определяя предельные допускаемые напряжения для различных материалов, используют зависимость между напряжениями при растяжении и напряжениями при кручении, которая для стали и чугуна имеет вид: для стали - [τкр] = 0,55....0,6 [σр] для чугуна - [τкр] = 1,0....1,2 [σр]) (здесь [σр] - справочная или определяемая экспериментально величина, (предельное допустимое напряжение растяжения) характеризующая материал бруса (вала).
Кроме требования прочности к валам предъявляются требования жесткости, которое заключается в том, что угол закручивания участка вала длиной 1 м не должен превышать предельной величины, определяемой требованиями конструкции. Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ0°]. Расчетная формула на жесткость при кручении имеет вид:
φ0°= 180 Мкр / (пGIr) ≤ [φ0°]
В реальных механизмах обычно допускаются углы закручивания валов в пределах [φ0°] = 0,25...1 градус/м.
43.Осевые моменты энергии. Моменты инерции некоторых Простейших сечений
Осевой момент инерции[0%9C%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8&veaction=edit&vesection=1"править | 0%9C%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8&action=edit§ion=1"править исходный текст]


Осевые моменты инерции некоторых тел.
Моментом инерции 0%9C%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0"механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n 0%9C%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D1%87%D0%BA%D0%B0"материальных точек системы на квадраты их расстояний до оси:
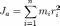 ,
,
где:
mi — масса i-й точки,
ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во 0%92%D1%80%D0%B0%D1%89%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5"вращательном движении вокруг оси подобно тому, как 0%9C%D0%B0%D1%81%D1%81%D0%B0"масса тела является мерой его инертности в 0%9F%D0%BE%D1%81%D1%82%D1%83%D0%BF%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5"поступательном движении.
 ,
,
где:
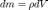 —
масса
малого элемента объёма тела
—
масса
малого элемента объёма тела  ,
, —
плотность,
—
плотность, —
расстояние
от элемента
до
оси a.
—
расстояние
от элемента
до
оси a.
Если тело однородно, то есть его 0%9F%D0%BB%D0%BE%D1%82%D0%BD%D0%BE%D1%81%D1%82%D1%8C"плотность всюду одинакова, то

Теорема Гюйгенса — Штейнера[0%9C%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8&veaction=edit&vesection=2"править | 0%9C%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8&action=edit§ion=2"править исходный текст]
Основная статья: 0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A8%D1%82%D0%B5%D0%B9%D0%BD%D0%B5%D1%80%D0%B0"Теорема Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от 0%9C%D0%B0%D1%81%D1%81%D0%B0"массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно 0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A8%D1%82%D0%B5%D0%B9%D0%BD%D0%B5%D1%80%D0%B0"теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела Jотносительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через 0%A6%D0%B5%D0%BD%D1%82%D1%80_%D0%BC%D0%B0%D1%81%D1%81"центр масс тела параллельно рассматриваемой оси, и произведения 0%9C%D0%B0%D1%81%D1%81%D0%B0"массы тела m на квадрат расстояния d между осями:
 ,
,
где  —
полная масса тела.
—
полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен: