
- •Связи и их реакции.
- •Геометрический способ нахождения равнодействующей плоской системы сходящихся сил
- •Аналитический способ нахождения равнодействующей плоской системы сходящихся сил
- •Пара сил. Момент пары сил
- •Момент силы относительно точки
- •Плоская система произвольно-расположенных сил. Условия равновесия
- •Формы уравнений равновесия плоской системы произвольно расположенных сил
- •Пространственная система сходящихся сил
- •Пространственная система произвольно расположенных сил
- •11.Момент силы относительной оси
- •12.Условия Пространственной системы произвольно расположенных сил
- •13.Центр тяжести. Способы определение центра тяжести. Координаты центра тяжести плоского тела и составленных сечений.
- •14.Скорость точки
- •15.Ускорение точки
- •16.Поступательные движения твердого тела
- •17.Вращательное движение твердого. Частные Случаи вращательного движения твердого тела.
- •18.Угловая скорость.19Угловое ускорение
- •20.Основные формулы равномерного и равномерно-переменного движения
- •Графики прямолинейного равномерного движения.
- •21.Сложные движения твердого тела. Плоскопараллельное движение. Мгновенные центра скоростей.
- •2.2. Описание движений твердого тела
- •2.3 Плоскопараллельное движение твердого тела
- •23.Аксиомы динамики
- •24.Методы кинематики
- •25.Работа при постоянной силе при прямолинейном движении, при вращательном движении. Работы силы тяжести
- •4.3 Работа постоянной силы на прямолинейном перемещении
- •26.Мощность.Кпд. А. Трение скольжение b.Трение Качение
- •27.Общие теоремы динамик
- •28.Основные уравнения динамики для вращательного движения твердого тела
- •29.Основные гипотезы и допущения сопротивлении материалов
- •30.Методи сечения
- •31.Внутненние силы в поперечном сечении
- •32.Напряжение полное, нормальное, касательное.
- •33.Растяжение, сжатие. Продольные силы и их эпюры.
- •Продольное сжатие
- •34.Нормальные напряжения и их эпюры
- •35.Условия прочности при растяжении, сжатии. Допускаемые напряжения.
- •36.Закон Гука при растяжении, сжатии.
- •37.Срез и смятие. Основные допущения на срез и смятия.
- •38.Расчет на срез и смятие
- •39.Кручение. Деформация при кручении
- •40.Правила построение эпюр крутящий момент.
- •41.Напряжение при кручении
- •42.Расчет на прочность и сжатие при кручении
- •43.Осевые моменты энергии. Моменты инерции некоторых Простейших сечений
- •44.Полярный момент инерции. Полярный момент инерции для круга, для кольца.
- •45.Изгиб. Основные понятия
- •46.Поперечные силы. Правила построение эпюр поперечных сил.
- •47.Изгибающие моменты. Правила построение эпюр изгибающий момент.
- •3.5. Построение эпюр изгибающих моментов и поперечных сил.
- •48.Диффиринциальная зависимость интенсивностью распространению нагрузки, поперечной силой и изгибающим моментом.
- •49. Расчет на прочность при изгибе.
- •50.Гипотизы прочности при изгибе.
- •51.Критическая сила для сжатие стержней
- •2.6.1. Критическая сила
- •52.Условия устойчивости для сжатых стержней
- •53.Основные критерии работоспособности и расчете деталей машин.
- •54.Основные кинематические и силовые соотношения в механических передачах.
- •55.Фрикционне передачи. Их достоинство и недостатки. Область применение, классификации.
- •Раздел 13. Фрикционные передачи.
- •Передача с катками клинчатой формы
- •56.Зубчатые передачи. Их достоинство и недостатки. Область применение, классификации.
- •57.Виды разрушений зубьев
- •58.Материялы зубчатых колес
- •4.3.1 Материалы, применяемые для изготовления зубчатых колес
- •59.Сылы, действующие в зацеплении зубчатых передач
- •1.6.1. Основы теории зацепления
- •60.Расчет прямозубых цилиндрических колес на усталость.
- •61.Передача винт-гайка. Достоинство и недостатки. Область применения.
- •5.1 Назначение и область применения передачи винт-гайка
- •5.2 Достоинства передачи винт-гайка
- •5.3 Недостатки передачи винт-гайка
- •62.Червячная передача. Достоинство и недостатки. Область применения.
- •63.Ременная передача. Достоинство и недостатки. Область применения, классификация.
- •64.Силы действующих в ременных передачах. Скольжение ремня
- •§ 17.4. Скольжение ремня. Передаточное число
- •65.Цепные передачи. Достоинства и недостатки. Область применения.
- •8.1 Назначение и область применения цепных передач
- •8.2 Достоинства цепных передач
- •8.3 Недостатки цепных передач
- •66.Силы действующие в цепных передачах.
- •67.Оси и валы. Расчет волов и осей на прочность. Валы и оси. Основы расчета на прочность, жесткость и выносливость
- •68.Подшипники скольжения. Их достоинства и недостатки. Область применения.
- •69.Подшипники качения. Их достоинства и недостатки. Область применения.
- •70.Класификация подшипников качения
- •71.Классификация муфт
- •72.Неразъемные соединения. Общие сведения. Общие сведения сварных соединений
- •Преимущества сварного соединения
- •Недостатки сварного соединения
- •Виды сварных соединений
- •Геометрия сварного шва
- •Критерии работоспособности сварных соединений
- •73.Расчет на прочность сварных соединений.
- •74.Резьбовые соединения
30.Методи сечения
Метод сечений позволяет определить внутренние силы, которые возникают встержне, находящемся в равновесии под действием внешней нагрузки.
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).
Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
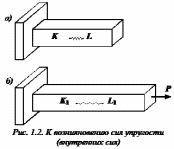 Приложим
теперь к стержню растягивающую силу
Приложим
теперь к стержню растягивающую силу 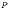 (рис.
1.2, б).
Пусть в результате деформации стержня,
частица K перейдет
в положение
(рис.
1.2, б).
Пусть в результате деформации стержня,
частица K перейдет
в положение 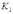 ,
а частица L
– в
положение
,
а частица L
– в
положение  .
Соединяющая эти частицы пружинка при
этом растянется. После снятия внешней
нагрузки частицы вернутся в первоначальное
положение K и Lблагодаря
усилию, которое возникло в пружинке.
Сила, которая возникла между частицами
(в пружинке) в результате деформации
идеально упругого стержня, называются
силой упругости или
внутренней силой. Она может быть
найдена методом
сечений.
.
Соединяющая эти частицы пружинка при
этом растянется. После снятия внешней
нагрузки частицы вернутся в первоначальное
положение K и Lблагодаря
усилию, которое возникло в пружинке.
Сила, которая возникла между частицами
(в пружинке) в результате деформации
идеально упругого стержня, называются
силой упругости или
внутренней силой. Она может быть
найдена методом
сечений.
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.
Разрежем стержень,
находящийся в равновесии под действием
некоторой системы сил 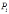 (рис.
1.3, а) на две части плоскостью,
перпендикулярной к его оси z.
(рис.
1.3, а) на две части плоскостью,
перпендикулярной к его оси z.
Отбросим одну из частей стержня и рассмотрим оставленную часть.
Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).
31.Внутненние силы в поперечном сечении


32.Напряжение полное, нормальное, касательное.
Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м2 (МПа = 106 Н/м2, кгс/см2=98 066 Па ≈ 105Па, тс/м2 и т. д.).
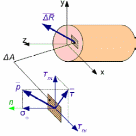 Рассечем
тело произвольным сечением Выделим
небольшую площадку ∆A.
Внутреннее усилие, действующее на нее,
обозначим∆R
Рассечем
тело произвольным сечением Выделим
небольшую площадку ∆A.
Внутреннее усилие, действующее на нее,
обозначим∆R .
Полное среднее напряжение на этой
площадке р
=∆R
.
Полное среднее напряжение на этой
площадке р
=∆R
 ∆A .
Найдем предел этого отношения при ∆A
∆A .
Найдем предел этого отношения при ∆A 0 .
Это и будет полным напряжение на данной
площадке (точке) тела.
0 .
Это и будет полным напряжение на данной
площадке (точке) тела.
p
=lim A
A 0
A
R
0
A
R
Полное
напряжение p
,
как и равнодействующая внутренних сил,
приложенных на элементарной площадке,
является векторной величиной и может
быть разложено на две составляющие:
перпендикулярное к рассматриваемой
площадке – нормальное
напряжение σn и
касательное к площадке – касательное
напряжение  n.
Здесь n –
нормаль к выделенной площадке1.
n.
Здесь n –
нормаль к выделенной площадке1.
Касательное
напряжение, в свою очередь, может быть
разложено на две составляющие, параллельные
координатным осям x,
y,
связанным с поперечным сечением
–
nx ny.
В названии касательного напряжения
первый индекс указывает нормаль к
площадке,второй индекс — направление
касательного напряжения.
ny.
В названии касательного напряжения
первый индекс указывает нормаль к
площадке,второй индекс — направление
касательного напряжения.
p
=

 n
nx
nx
n
nx
nx 

Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением p , а с его составляющими σx xy xz . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.
