27.Общие теоремы динамик

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ

В предыдущей главе, мы рассматривали дифференциальные уравнения движения точки и некоторые результаты их интегрирования, то есть получения уравнений движения типа  .

Более чем трехсотлетний опыт интегрирования дифференциальных уравнений движения скопился в так называемых общих теоремах динамики.

В динамике, часто вместо основного закона, удобно пользоваться его следствиями. Следствия сформулированы в виде общих теорем. Они позволяют установить наглядную зависимость между основными динамическими характеристиками, изучать части процесса не затрагивая целого, избавляют от интегрирования, так как сами теоремы результат интегрирования в конкретных случаях.

1 . Количество движения, импульс силы и кинетическая энергия.

Векторная величина 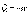  равная произведению массы точки на вектор ее скорости называется количеством движения точки. Направлен вектор 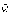  так же, как и скорость   точки.

равная половине произведения массы точки на квадрат ее скорости называется кинетической энергией точки.

Элементарным импульсом силы называется векторная величина 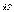 , равная произведению вектора силы   на элементарный промежуток времени.

Тогда импульс силы за конечный промежуток времени  :

а если сила постоянна по модулю и направлению, то

Через проекции на оси координат импульс выражается как

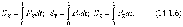
28.Основные уравнения динамики для вращательного движения твердого тела

Согласно уравнению (5.8) второй закон Ньютона для вращательного движения

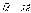
По определению угловое ускорение   и тогда это уравнение можно

переписать следующим образом

с учетом (5.9)

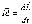
или

(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 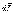 , равно импульсу момента  всех внешних сил, действующих на это тело.

29.Основные гипотезы и допущения сопротивлении материалов

ОСНОВНЫЕ ГИПОТЕЗЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

При построении теории расчета невозможно отразить все многообразие свойств реальных материалов, поэтому приходится делать целый ряд допущений, упрощающих расчеты.

В курсе сопротивления материалов рассматривается идеализированное тело, которое считается сплошным (без пустот) и однородным.  Это означает, что свойства материала не зависят от формы и размера тела и одинаковы во всех его точках. Упругие свойства материала во всех направлениях одинаковы, т.е. материал тела обладает упругой изотропией. Тело считается абсолютно упругим, если после устранения причин, вызывающих деформацию, оно полностью восстанавливает свои первоначальные форму и размеры.  Это допущение справедливо лишь при напряжениях, не превышающих предел упругости. Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке (закон Гука).  Закон Гука справедлив лишь при напряжениях, не превышающих предел пропорциональности. Деформации элементов конструкции в большинстве случаев настолько малы, что можно не учитывать их влияние на взаимное расположение нагрузок и на расстояние от нагрузок до любых точек конструкции. Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности (принцип независимости действия сил). Принцип независимости действия сил не распространяется на работу внешних и внутренних сил и на потенциальную энергию. Поперечное сечение, плоское до деформации, остается плоским и после деформации (гипотеза плоских сечений Бернулли)