25.Работа при постоянной силе при прямолинейном движении, при вращательном движении. Работы силы тяжести

Работа W постоянной силы F при прямолинейном движении точки ее приложения равна произведению модуля силы F на расстояние s и на косинус угла между направлением силы и направлением перемещения, т. е.

Угол α между направлением силы и направлением движения может меняться в пределах от 0 до 180°. При α < 90° работа положительна, при α > 90° — отрицательна, при α = 90° W = 0 (работа равна нулю).

Еcли cила составляет с направлением движения острый угол, она называется движущей силой, ее работа всегда положительна. Если угол между направлениями силы и перемещения тупой, сила оказывает сопротивление движению, совершает отрицательную работу и носит название силы сопротивления. Примерами сил сопротивления могут служить силы резания, трения, сопротивления воздуха и другие, которые всегда направлены в сторону, противоположную движению.

Когда α = 0, т. е. когда направление силы совпадает с направлением скорости, W = Fs, так как cos α = 1. Произведение F cos α есть проекция силы F на направление движения материальной точки. Следовательно, работу силы можно определить как произведение перемещения s и проекции силы F на направление движения точки.

За единицу работы в Международной системе единиц (СИ) принят джоуль (Дж), равный работе силы в один ньютон (Н) на совпадающем с ней по направлению движения длиной в один метр (м): . Применяется также более крупная единица работы — килоджоуль (кДж), 1 кДж = 1000 Дж = 10³Дж. В технической системе (МКГСС) за единицу работы принят килограмм-сила метр (кгс*м)

Произведение силы на перемещение и на косинус угла между ними  A=F*s*cosa

4.3 Работа постоянной силы на прямолинейном перемещении

 

Определим работу для случая, когда действующая сила постоянна по величине и направлению, а точка ее приложения перемещается по прямолинейной траектории. Рассмотрим материальную точку С, к которой приложена постоянная по значению и направлению сила F.

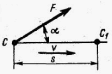
За некоторый промежуток времени t точка С переместилась в положение С1 по прямолинейной траектории на расстояние s.

Работа W постоянной силы F при прямолинейном движении точки ее приложения равна произведению модуля силы F на расстояние s и на косинус угла между направлением силы и направлением перемещения, т. е.

Угол ? между направлением силы и направлением движения может меняться в пределах от 0 до 180°. При ? < 90° работа положительна, при ? > 90° — отрицательна, при ? = 90° W = 0 (работа равна нулю).

Еcли cила составляет с направлением движения острый угол, она называется движущей силой, ее работа всегда положительна. Если угол между направлениями силы и перемещения тупой, сила оказывает сопротивление движению, совершает отрицательную работу и носит название силы сопротивления. Примерами сил сопротивления могут служить силы резания, трения, сопротивления воздуха и другие, которые всегда направлены в сторону, противоположную движению.

Когда ? = 0, т. е. когда направление силы совпадает с направлением скорости, W = Fs, так как cos ? = 1. Произведение F cos ? есть проекция силы F на направление движения материальной точки. Следовательно, работу силы можно определить как произведение перемещения s и проекции силы F на направление движения точки.

За единицу работы в Международной системе единиц (СИ) принят джоуль (Дж), равный работе силы в один ньютон (Н) на совпадающем с ней по направлению движения длиной в один метр (м):  . Применяется также более крупная единица работы — килоджоуль (кДж), 1 кДж = 1000 Дж = 10?Дж. В технической системе (МКГСС) за единицу работы принят килограмм-сила метр (кгс*м).

 

Работа силы тяжести

Гипермаркет знаний>>0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0_%D0%B8_%D0%B0%D1%81%D1%82%D1%80%D0%BE%D0%BD%D0%BE%D0%BC%D0%B8%D1%8F"Физика и астрономия>>0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0_10_%D0%BA%D0%BB%D0%B0%D1%81%D1%81"Физика 10 класс>>Физика: Работа силы тяжести

   Вычислим работу, используя в этот раз не 0%92%D1%82%D0%BE%D1%80%D0%BE%D0%B9_%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0"второй закон Ньютона, а явное выражение для сил взаимодействия между телами в зависимости от расстояний между ними. Это позволит нам ввести понятие потенциальной энергии - энергии, зависящей не от скоростей тел, а от расстояний между телами (или от расстояний между частями одного и того же тела).    Вычислим сначала работу силы тяжести при падении тела (например, камня) вертикально вниз. В начальный момент времени тело находилось на высотеh₁ над поверхностью Земли, а в конечный момент времени - на высотеh₂ (рис.6.5). Модуль перемещения тела  .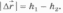

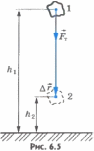
   Направления векторов силы тяжести   и перемещения   совпадают. Согласно определению работы (см. формулу (6.2)) имеем

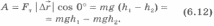
   Пусть теперь тело бросили вертикально вверх из точки, расположенной на высоте h₁,над поверхностью Земли, и оно достигло высоты h₂ (рис.6.6). 

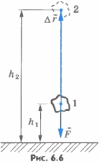
Векторы 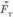  и   направлены в противоположные стороны, а модуль перемещения  . Работу силы тяжести запишем так:

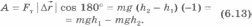
   Если же тело перемещается по прямой так, что направление перемещения составляет угол   с направлением силы тяжести (рис.6.7), то работа силы тяжести равна:

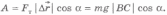
Из прямоугольного треугольника BCD видно, что  . Следовательно,

   Формулы (6.12), (6.13), (6.14) дают возможность подметить важную закономерность. При прямолинейном движении тела работа силы тяжести в каждом случае равна разности двух значений величины, зависящей от положений тела в начальный и конечный моменты времени. Эти положения определяются высотами h₁ и h₂ тела над поверхностью Земли.    Более того, работа силы тяжести при перемещении тела 0%92%D1%82%D0%BE%D1%80%D0%BE%D0%B9_%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0._%D0%9C%D0%B0%D1%81%D1%81%D0%B0"массой m из одного положения в другое не зависит от формы траектории, по которой движется тело. Действительно, если тело перемещается вдоль кривой ВС (рис.6.8), то, представив эту кривую в виде ступенчатой линии, состоящей из вертикальных и горизонтальных участков малой длины, увидим, что на горизонтальных участках работа силы тяжести равна нулю, так как сила перпендикулярна перемещению, а сумма работ на вертикальных участках равна работе, которую совершила бы сила тяжести при перемещении тела по вертикальному отрезку длиной h₁-h₂.

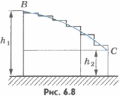
Таким образом, работа при перемещении вдоль кривой ВС равна:

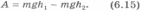
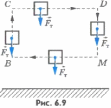
   При движении тела по замкнутой траектории работа силы тяжести равна нулю. В самом деле, пусть тело движется по замкнутому контуру ВСDМВ (рис.6.9). На участках ВСи DМ сила тяжести 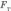  совершает работы, равные по абсолютной величине, но противоположные по знаку. Сумма этих работ равна нулю. Следовательно, равна нулю и работа силы тяжести на всем замкнутом контуре.

   Силы, обладающие такими свойствами, называют консервативными.    Итак, работа силы тяжести не зависит от формы траектории тела; она определяется лишь начальным и конечным положениями тела. При перемещении тела по замкнутой траектории работа силы тяжести равна нулю.