2. Математические модели сау

2.1. Построение модели элемента системы управления

В главе 1 мы ознакомились с основными элемен­тами системы автоматического управления и с поня­тием математической модели объекта управления. Математическая модель элемента системы управле­ния - это уравнение или система уравнений, описы­вающих зависимость выходной величины y(t) эле­мента от входной величины x(t) этого элемента и возмущающих воздействий (помех).

Математическая модель реального элемента или системы является некоторой абстракцией, которая от­ражает лишь наиболее существенные свойства иссле­дуемой реальной системы. При построении математи­ческой модели, с одной стороны, желательно воз­можно точнее отразить свойства объекта; с другой стороны, сложность получаемых при этом уравнений существенно затрудняет нахождение и исследование их решений. В то же время при излишнем упрощении, то есть пренебрежении рядом свойств системы, можно существенно исказить имеющую место в действитель­ности картину. Поэтому при построении модели при­ходится идти на компромисс между стремлением к более точному описанию и возможностью эффек­тивного анализа полученных решений.

Математические модели системы разрабатываются для следующих вариантов использования:

- для исследования реальной системы;

- для проектирования системы управления;

- для использования в процессе управления, на­пример, в самонастраивающихся системах (см. гл. 9).

Математическая модель строится на основе ис­пользования физических законов, определяющих ха­рактер протекающих в модели процессов. Так, для механических систем модель составляется на основе за­конов механики, аэродинамики, принципа Даламбера - Лагранжа и т. п.

2.2. Динамические и статические звенья сау

Система автоматического управления состоит из отдельных элементов (электродвигателей, усилителей, измерительных устройств и так далее). Каждый из элемен­тов замкнутой автоматической системы соединен с другим элементом системы так, что его выходная ве­личина является входной величиной другого элемен­та системы. Выходная величина элемента может от­личаться от его входной величины как физической природой, так и характером изменения во времени. Например, для термопары входной величиной являет­ся температура, а выходной - напряжение (эдс тер­мопары).

Воздействия отдельных элементов автоматической системы друг на друга часто являются односторон­ними, то есть предыдущий элемент воздействует на последующий, не воспринимая при этом обратного воздействия. Например, напряжение на выходе тер­мопары электрического термометра зависит от темпе­ратуры, а последняя не зависит от величины электро­движущей силы термопары. Такое свойство элемента называется однонаправленностью, а соответствующий элемент называется элементом направленного дей­ствия.

При построении функциональной схемы САУ си­стема разбивается на элементы направленного дейст­вия в соответствии с теми функциями, которые они выполняют (чувствительный элемент, элемент срав­нения, исполнительный элемент и так далее).

Для получения математического описания системы управления ее расчленяют на элементы направленного действия (звенья) так, чтобы можно было сравни­тельно просто получить их математическое описание.

Звеном называют часть системы, которая осущест­вляет некоторое преобразование входной величины в выходную. Следует отметить, что разбиение системы на звенья может не совпадать с разбиением системы на функциональные элементы. Звено - это условно выделенный направленного действия преобразователь сигналов, который может быть частью элемента авто­матики или состоять из нескольких таких элементов.

В отличие от элемента автоматики, звено не обя­зательно конструктивно или схемно оформлено (на­пример, якорные обмотки электродвигателей, отдель­ные каскады усилителей). В отдельных случаях эле­ментарное звено физически не может быть выделено из системы и характеризует лишь некоторую матема­тическую зависимость между некоторыми величинами в системе автоматического управления.

Если разбить систему на звенья направленного действия, то математическое описание каждого звена может быть выполнено без учета его связей с другими звеньями системы. При этом математическое описание всей системы в целом может быть получено как сово­купность составленных независимо друг от друга ура­внений звеньев системы и уравнений связи между звеньями. Уравнениями связи называют уравнения, отражающие характер передачи воздействия между звеньями системы.

После разбиения САУ на звенья направленного действия и получения математического описания звеньев составляется структурная схема. Структур­ной схемой системы автоматического управления на­зывается схема, показывающая, из каких звеньев со­стоит система и как эти звенья соединены между со­бой. На структурной схеме звенья изображаются пря­моугольниками, а связи между звеньями и внешние воздействия показываются стрелками. Каждому зве­ну структурной схемы придается описывающее его уравнение или характеристика.

На рис. 2.1 приводятся две структурные схемы. На рис. 2.1, а показана схема САУ, состоящая из трех звеньев. Зависимость между выходной величиной пер­вого звена y₁ и его входной величиной х₁ задана вы­ражением A₁, зависимость между у₂ и х₂ задана вы­ражением А₂. Нелинейная зависимость между у₃ и х₃ для третьего звена задана в виде графика. Внешнее воздействие на второе звено показано стрелкой f₂. Кружком с секторами условно обозначен элемент сравнения - суммирующее звено. Его выходная вели­чина, являющаяся входом первого звена, равна раз­ности х₁=и-у₃. Зачерненный сектор соответствует вычитаемому сигналу. На рис. 2.1, б изображена часть системы, состоящая из двух звеньев - дифференцирующего и релейного.

Статическая характеристика звена представляет собой зависимость между входной х и выходной у ве­личинами в установившемся режиме при разных по­стоянных значениях внешнего воздействия f(t) = f.

Возьмем в качестве примера электрический двига­тель постоянного тока с независимым возбуждением (рис.2.2,а). Здесь входной величиной является ток якоря i_я, выходной величиной - угловая скорость ω, а внешним воздействием - момент нагрузки на валу М_н и напряжение питания независимого возбуждения и_п (рис. 2.2,б).

Один из многих возможных режимов работы дви­гателя (постоянные величины М_н и и_п) называется но­минальным, на который, как правило, и рассчитана работа двигателя. При этих значениях и счи­таем, что f = 0. Отклонение величин М_н и и_п от но­минальных, которое может произойти независимо от работы системы управления, будет представлять со­бой внешнее воздействие f(t).

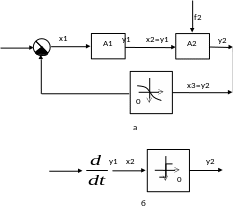
Рисунок 2.1

Рисунок 2.2

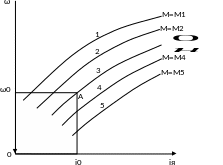
Рисунок 2.3

Построим статическую характеристику ω = ω(i_я) этого звена при f = 0, то есть при М_н= и и_п= (линия 3 на рис. 2.3). Ее можно построить расчетным путем на основе теории электрических машин или же получить экспериментально. Точка А соответствует номинальному значению угловой скорости ω₀ и номи­нальному значению тока якоря i₀. При увеличении нагрузки на валу (М_н< ) статическая характери­стика переместится вниз (кривые 4 и 5 на рис. 2.3), а при уменьшении нагрузки кривые ω(i_я) будут прохо­дить выше (кривые 1 и 2 на рис. 2.3).

Рисунок 2.4

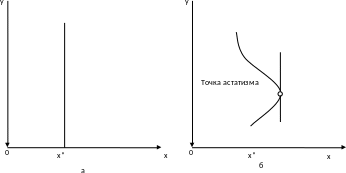
Рисунок 2.5

В общем случае зависимость установившегося зна­чения выходной величины у от установившегося зна­чения входной величины х является нелинейной (рис. 2.3). Угловой коэффициент k_o, образуемый каса­тельной к статической характеристике в любой точке А, называется коэффициентом усиления: k_o= dy/dx. Из рис. 2.4 видно, что k =r tga, где r - коэффициент, зависящий от принятых масштабов по осям х и y. Значение k₀ служит мерой статизма звена.

Если k₀ =∞, то звено называют астатическим. Астатическое звено при некотором значении входной величины х=х* нахо­дится в равновесии при любом значении вы­ходной величины у (рис. 2.5, а). Точка ста­тистической характе­ристики, в которой касательная вертикаль­на (k=∞), называ­ется точкой астатизма (рис. 2.5, б).

Динамическая характеристика звена. Статические характеристики звена (системы) описывают лишь поведение звена (системы) в установившемся режиме. Если на нахо­дящееся в некотором состоянии звено (систему) подействует некоторое возмущающее воздействие, то оно начнет

переходить в некоторое другое состояние. Характер процесса перехода системы или звена си­стемы из одного состояния в другое определяется

динамической характеристикой звена (уравнением движения). Уравнение движения звена - это уравне­ние (обычно дифференциальное), определяющее изме­нение во времени выходной величины звена по задан­ному изменению во времени его входной величины.

Дифференциальные уравнения звеньев системы мо­гут быть разными. Для звеньев с сосредоточенными параметрами общее уравнение имеет вид

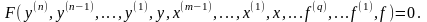(2.2.1)

Здесь m, n, q - натуральные числа, показывающие высший порядок производных от входной величины х, выходной величины у и внешнего воздействия f. На практике в большинстве случаев m < п и q < п. Чис­ло п называется порядком дифференциального урав­нения (2.2.1). При п=1 имеем дифференциальное уравнение 1-го порядка:

(2.2.2)

при п=2 - 2-го порядка:

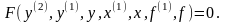(2.2.3)

Уравнение статической характеристики звена мож­но получить из уравнения (2.2.1), положив все произ­водные по времени равными нулю:

F (0, 0, ... , 0, у, 0, ... , 0, х, 0, 0, ... , f) = 0. (2.2.4)

Это уравнение определяет статическую характери­стику звена в неявном виде.

Если динамика звена описывается линейным диф­ференциальным уравнением, то это звено называют линейным; если дифференциальное уравнение нели­нейно, то звено называют нелинейным. Для линейных звеньев характерно, что реакция звена на линейную комбинацию воздействий равна той же линейной ком­бинации реакций звена на каждое влияние в отдельности. Это свойство линейных звеньев выражает со­бой принцип суперпозиции.

В связи с тем, что решение нелинейного дифферен­циального уравнения в общем случае - задача значительно более сложная, чем решение линейного диф­ференциального уравнения, для упрощения исследова­ния, когда это возможно, желательно заменить нели­нейное дифференциальное уравнение приближенным линейным, решение которого с достаточной степенью точности описывает свойства исходной нелинейной си­стемы. Процесс замены нелинейного дифференциаль­ного уравнения линейным называется линеаризацией.

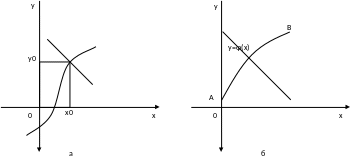
Рисунок 2.6

Если дифференциальное уравнение звена нелиней­но из-за нелинейности его статической характеристи­ки, то для линеаризации уравнения необходимо за­менить нелинейную статическую характеристику у=φ(х) линейной функцией у=ах+b. Линеаризация осуществляется при помощи разложения в ряд Тей­лора функции y=φ(х) в окрестности некоторой точ­ки (х₀,y₀) статической характеристики и отбрасыва­нием всех членов, содержащих отклонения Δy в сте­пени выше первой. Это означает замену кривой y=φ(х) касательной в точке х₀, y₀ (рис. 2.6, а). В от­дельных случаях линеаризация осуществляется путем проведения секущей (прямая АВ на рис. 2.6, б). Нели­нейные статические характеристики звена, линеари­зуемые таким образом в требуемом диапазоне измене­ния входной величины, называют несущественно не­линейными характеристиками.

В системах автоматики часто встречаются звенья, характеристики которых не поддаются такой лине­аризации; в частности, к ним относятся звенья, характеристики которых нельзя разложить в ряд Тей­лора в окрестности точки, соответствующей устано­вившемуся состоянию. Такие характеристики называ­ют нелинеаризуемыми или существенно нелинейными.

Существенно нелинейные элементы (звенья), наличие которых делает систему ав­томатического управления нелинейной, могут быть раз­делены на две группы:

а) элементы, обладаю­щие нелинейными однозна­чными характеристиками (однозначные нелинейные элементы);

б) элементы, обладаю­щие линейными многознач­ными характеристиками (многозначные нелинейные элементы).

Однозначным нелиней­ным элементом называют элемент, статическая ха­рактеристика которого поз­воляет по величине входно­го сигнала однозначно оп­ределить величину выходно­го сигнала.

Наиболее часто встречающиеся типы однозначных нелинейных элементов приведены на рис.2.7.

Элемент, изображенный на рис. 2.7, а, называется одно­значным нелинейным элементом с зоной нечувстви­тельности. Он может быть охарактеризован следую­щим образом:

(2.2.5)

где k=tgφ.

Элемент, изображенный на рис. 2.7,б, называется однозначным нелинейным элементом с насыщением.

Он описывается следующим образом:

(2.2.6)

где k=tgφ.

На рис.2.7,в показан идеальный релейный эле­мент. Его математическое описание

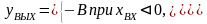(2.2.7)

Представление о релейном элементе с зоной нечув­ствительности дает рис. 2.7, г. Его математическое описание

(2.2.8)

Рисунок 2.7

Многозначным нелинейным элементом называют элемент с такой статической характеристикой, по ко­торой связь между входным и выходным сигналом зависит от предыстории, то есть от изменений (увеличе­ния или уменьшения) входного сигнала. Наиболее ти­пичными многозначными элементами являются эле­менты, обладающие гистерезисом. На рис. 2.8 показано три таких элемента. Наглядное представление о свойствах нелинейных элементов можно получить из рис. 2.9, на котором показано прохождение гармони­ческого входного сигнала через однозначный нелинейный элемент с зоной нечувствительности (а), идеаль­ный релейный элемент (б) и через элемент с гистере­зисом (в).

Рисунок 2.8

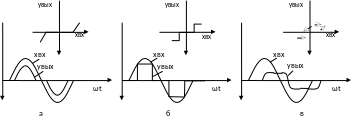
Рисунок 2.9

Замена характеристики существенно нелинейного звена прямой линией с постоянным углом наклона мо­жет привести к значительным ошибкам в описании происходящих в звене процессов.