9. Современные тенденции развития систем управления

9.1. Управление при неполной начальной информации

В главе 1 говорилось, что часто характеристики уп­равляемого объекта и действующих на него возмуще­ний значительно и заранее непредвиденным образом изменяются во время процесса управления. Кроме того, имеются такие объекты, динамические характе­ристики которых заранее практически неизвестны или не могут быть достаточно просто определены. В этих случаях одной исходной информации недостаточно для управления. Системы управления такими объек­тами относятся к системам с неполной начальной ин­формацией об управляемом объекте. В этом случае, чтобы качественно управлять объектом, необходимо автоматически в процессе работы пополнять инфор­мацию об объекте и возмущающих воздействий. Информацию, необходимую для управления и получае­мую в процессе работы системы, называют рабочей, или текущей информацией.

Системы управления, в которых способ функциони­рования управляющего устройства автоматически целенаправленным образом изменяется для осущест­вления наилучшего управления объектом, называются адаптивными (или самоприспосабливающимися). Автоматическое изменение способа функционирования управляющего устройства называют адаптацией или настройкой самоприспосабливающейся системы. На­стройка осуществляется путем изменения: параметров управляющего устройства; структуры управляющего устройства; алгоритма управления.

В адаптивных САУ необходимо иметь устройство для пополнения информации об управляемом объекте и возмущающих воздействиях, а также устройство для осуществления настройки системы. Адаптивные системы, у которых целенаправленно изменяются па­раметры управляющего устройства, называются самонастраивающимися; если изменяются параметры и структура управляющего устройства, то системы на­зываются самоорганизующимися; если параметры, структура и алгоритм управления меняются с исполь­зованием опыта функционирования системы, то систе­мы называются самообучающимися.

9.2. Экстремальные сау

Простейшим видом самонастраивающихся систем (СНС) являются системы экстремального управления (СЭУ). Экстремальными системами называют систе­мы, которые в процессе работы автоматически отыски­вают такие управляющие воздействия на входе управ­ляемого объекта, при которых обеспечивается непре­рывное поддержание показателя качества системы вблизи его экстремального значения. Основная осо­бенность этих

систем состоит в том, что управление в них осуществляется не путем компенсации частных рассогласований (отклонений) в системе, а целенаправленным воздействием на систему с учетом неко­торой функции ее состояния - показателя качества системы управления.

Системы экстремального управления сложнее обычных САУ, и их целесообразно применять, если объект управления имеет достаточно ясно выражен­ный экстремум показателя качества, который сущест­венно зависит от управляющих воздействий и внеш­них условий. На рис. 9.1 проиллюстрирована зависимость пока­зателя качества I от управляющего воздействия для различных вариантов внешних условий. Если при из­менении внешних условий изменяется только величина экстремального значения показателя качества I_э, а ко­ордината и_э, соответствующая экстремуму, не изме­няется, или изменяется только координата u_э, соответ­ствующая экстремуму I_э, а величина I_э не изменяется, то можно обеспечить экстремальное значение по­казателя качества, используя обычную САУ, то есть САУ с постоянными параметрами управляющего устройства.

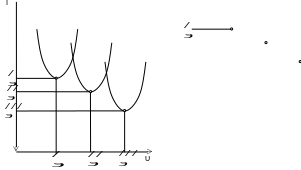
Рисунок. 9.1

Показателем качества в СЭУ могут быть различ­ные величины. Например, для системы управления металлорежущим станком таким

показателем может являться производительность, которая определяется весом стружки, снимаемой резцом в единицу времени, при условии, что температура резца и детали не пре­высит заданного уровня.

Обычно показатель качества в СЭУ является функ­цией нескольких управляющих воздействий, то есть I=I(u₁,...,и_п). Если эта функция дифференцируема и искомый оптимум заведомо не лежит на границе, то для отыскания экстремума ее можно применить ме­тоды, рассмотренные в предыдущей главе.

Для определения градиента на практике часто применяют метод синхронного детектирования. Этот метод позволяет одновременно найти все составляю­щие градиента. При определении частных производ­ных ∂I/∂u_i этим методом (рис. 9.2) входные перемен­ные объекта модулируются небольшими по амплитуде, гармоническими колебаниями различных частот, то есть к сигналам и₁, . . . , и_п добавляются синусоидальные сигналы

Δu_i = a_isinω_it (i=1,2,...,п) (9.2.1)

различных частот ω₁,...,ω_n. Для определения влия­ния колебаний каждой переменной на критерий каче­ства I используются синхронные детекторы.

Каждый детектор выполняет умножение величины I на соот­ветствующий гармонический сигнал a_isinω_it и усред­нение полученного произведения по времени. При этом выходные сигналы синхронных детекторов приблизительно пропорциональны частным производным функции I по соответствующим переменным.

Рисунок 9.2

Действительно, при малых амплитудах а₁,а₂,...,а_п функцию I можно разложить в ряд Тейлора по приращениям Δu_i. Если ограничиться членами пер­вой степени относительно Δu_i, то

(9.2.2)

Умножая это равенство на a_isinω_it и осредняя ре­зультат по времени, получим

(9.2.3)

Если взять время осреднения Т кратным всем перио­дам 2π/ω₁,...,2π/ω_n и достаточно большим, то фор­мула (9.2.3) может быть переписана в виде

(i=l, 2, ...,n). (9.2.4)

В качестве поисковых колебаний Δu_i - системы мо­жно использовать не только синусоидальные колеба­ния, но и любые типы колебаний, удовлетворяющие единственному условию, чтобы средние значения произведений колебаний различных параметров за время осреднения были достаточно близки к нулю.

По источнику колебаний, используемых для вычис­ления градиента функции, СЭУ подразделяются на: системы с автоколебательным поиском экстремума: системы с принудительным поиском экстремума.

После того как найден градиент функции I, необ­ходимо организовать движение системы к точке экс­тремума, то есть поиск экстремума. В настоящее время имеется большое число методов решения этой задачи.

Классификация СЭУ. В настоящее время имеется большое количество видов экстремальных систем, и классификацию их можно проводить по разным при­знакам.

По источнику колебаний, используемых для вычис­ления градиента функции (по способу поиска), СЭУ подразделяются на: а) системы с автоколебательным поиском экстремума; б) системы с принудительным поиском экстремума.

Если поисковые колебания генерируются самой си­стемой, СЭУ называют экстремальной системой с ав­токолебательным поиском экстремума. Если поиско­вые колебания вводятся от специально для этой цели предусмотренного источника, то СЭУ называют экс­тремальной системой с принудительным поиском экс­тремума.

Рисунок 9.3

Рассмотрим в качестве примера принцип работы СЭУ с автоколебательным поиском экстремума I_э, схе­ма которой показана на рис. 9.3, а. На датчик показа­теля экстремума (ДПЭ) подается измеренное значение показателя качества, который непрерывно изме­няется (движется) по направлению к экстремуму при помощи монотонного изменения входной переменной и объекта управления (ОУ). При достижении показа­телем качества экстремального значения (дI/ди=0) ДПЭ фиксирует (запоминает) значение u_э, соответст­вующее экстремуму показателя качества, но никаких, управляющих сигналов не выдает. Величина и при этом продолжает изменяться в ту же сторону (для оп­ределенности пусть и увеличивается). Когда разность между текущим значением I и величиной I_э становит­ся равной некоторой заранее заданной величине (по­рогу) Δ (Δ=|I-I_э|), ДПЭ выдает импульс, вызы­вающий срабатывание реверсирующего устройства (РУ). При этом исполнительное устройство (ИУ) ме­няет направление изменения величины и (и начинает уменьшаться), и величина I(u) вновь стремится к экс­тремальному значению. В СЭУ такого вида возникает автоколебательный процесс около положения, соот­ветствующего экстремуму I.

Рассмотренная СЭУ является простейшей. Недо­статком ее является возможность «ложных реверсов» из-за широкополосных помех (рис. 9.3,б). Из-за по­мех реверс может происходить не около точки, соот­ветствующей экстремуму показателя качества (точ­ка А), а в любой другой точке, где градиент измерен­ного значения показателя качества обращается в нуль. Показатель качества в этой системе отклонен от экстремума. Уровень помех определяет величину порога Δ.

Более совершенные и сложные СЭУ описаны в спе­циальной технической литературе.