3.2. Линейные сау, описываемые обыкновенными дифференциальными уравнениями с постоянными коэффициентами

В этом разделе будут рассмотрены линейные САУ, описываемые системой уравнений вида

(3.2.1)

где элементы матриц A и В не зависят от времени, или уравнением вида

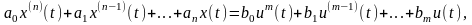(3.2.2)

где а_i (i=0,1,2, ..., п), b_j (j=0, 1, 2, .... m) - постоянные величины. Очевидно, что все положения, изложенные в предыдущих разделах данной главы, справедливы для уравнений (3.2.1) и (3.2.2).

3.2.1. Передаточная функция линейной САУ. Находим связь между лапласовыми изображениями реакции системы x(t) и входного воздействия на систему u(t):

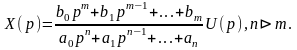(3.2.3)

Функция W(p)=X(p)/U(p), представляющая собой отношение преобразования Лапласа выходного сиг­нала линейной САУ к преобразованию входного сигнала при нулевых начальных условиях, называется передаточной функцией линейной САУ. Согласно (3.2.3)

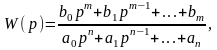(3.2.4)

где р=σ + iω и σ > σ₀ (σ₀ - абсцисса абсолютной сходимости) .

Смысл передаточной функции, как явствует из оп­ределения, заключается в том, что она представляет собой некий оператор, преобразующий внешнее воз­действие на входе в реакцию системы на выходе. Если известно обратное преобразование Лапласа, то есть , то, можно записать

(3.2.5)

Интеграл, стоящий в правой части (3.2.5) и опреде­ляющий выходной сигнал при нулевых начальных зна­чениях в виде свертки оригинала передаточной функ­ции и внешнего воздействия, называется интегралом Дюамеля.

Все сказанное выше относится к разомкнутым ли­нейным САУ. В случае если САУ является замкнутой (рис. 2.18) или, как говорят, охвачена обратной связью, то передаточная функция замкнутой САУ

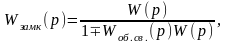(3.2.6)

где W_oб.св (р) - передаточная функция элементов об­ратной связи. Знак «плюс» соответствует отрицатель­ной обратной связи, а знак «минус» - положительной (см. также подглаву 4.6). Формула (3.2.6) легко получается из следующих соображений. Согласно определению передаточной функции

но, как видно из рис. 2.18, то есть

Разделив числитель и знаменатель на U₂(p), полу­чим

что и требовалось доказать.

Свойства передаточной функции:

1. 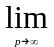W(p)=0. Это следует из требования n>т (см. (3.2.3)).

2. Так как a_i (i=0,I,2,...,п) и b_j (j=0,1,2,...,п) - вещественные величины, то нули и полю­сы (точки, в которых Х(р) обращается в бесконечность) - комплексно-сопряженные числа.

3. Корни полиномов

(3.2.7а)

(3.2.7б)

являются соответственно нулями и полюсами W(p)=K(p)/D(p).

3.2.2. Переходная функция. Сигнал h(t), получае­мый на выходе системы при подаче на его вход еди­ничного скачка u_o(t), называется переходной функцией системы. Согласно u₀(t)=1/p и, следовательно, по определению 3.2.3 имеем

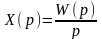. (3.2.8)

Переходя от изображения к оригиналу, получим

(3.2.9)

Найдем связь между передаточной и переходной функциями. Из формулы (3.2.5) при u(t)=u₀(t) сле­дует, что

(3.2.9a)

откуда

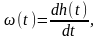(3.2.10)

то есть оригинал передаточной функции равен производ­ной от переходной функции системы. Не следует за­бывать, что, как и прежде, система имеет нулевые на­чальные условия.

Выразим x(t) - реакцию системы на произвольное воздействие u(t)- через переходную функцию h(t). Из (3.2.10) и (3.2.5) имеем

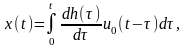
и, производя интегрирование по частям, получим

(3.2.11)

Здесь учтено, что h(0) =0.

3.2.3. Весовая, или импульсная переходная, функ­ция системы. Прежде чем дать определение весовой функции системы, рассмотрим функцию δ(t), назы­ваемую функцией Дирака или дельта-функцией. В теории автоматического управления эту функцию часто называют единичным импульсом. Смысл подоб­ного названия станет ясен из дальнейшего. Определим δ(t) следующими соотношениями:

(3.2.12) 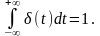(3.2.13)

Очевидно, что δ(t), так же как и u_o(t), является некой математической абстракцией реально существующих сигналов.

Свойства единичного импульса:

1. 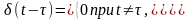(3.2.14а)

2. (3.2.14б)

3. (3.2.14в)

если f(t) - ограниченная и непрерывная функция.

Свойство (3.2.14в) дает возможность представить любой сигнал в виде совокупности единичных импуль­сов:

(3.2.15)

Этот же результат можно получить непосредственно из прямого преобразования Лапласа, приме­нение которого в данном случае возможно, так как δ(t) абсолютно интегрируема.

Сигнал, получаемый на выходе линейной САУ при подаче на ее вход единичного импульса, называется весовой, или импульсной переходной, функцией W(t). Так как δ(t)=1, то

X(p)=W(p). (3.2.16)

Переходя от изображения к оригиналу, получаем, что весовая функция системы есть оригинал передаточной функции.

Как следует из изложенного выше, передаточная, переходная и весовая функции системы, являющиеся ее характеристиками, однозначно связаны друг с дру­гом. Зная одну из них, всегда можно найти любую другую.

3.2.4. Частотные и логарифмические характеристики линейной САУ. Частотной характеристикой линей­ной САУ или, что эквивалентно, комплексной частот­ной функцией линейной САУ называется функция W(iω), получаемая из передаточной функции системы при подстановке p=iω. Физически эта подстановка означает, что сигнал на входе системы описывается гармонической функцией, то есть функцией вида x(t)= х₀е^iωt.

Частотную характеристику W(iω), как и любую другую функцию комплексного переменного, можно представить в виде

W(iω)=R(ω)+iI(iω), (3.2.17)

где

R (ω) = Re{W(iω)}, (3.2.18a)

I(ω)=Im{W(iω)}, (3.2.18б)

Формула (3.2.17) показывает, что W(iω) является век­торной (геометрической) суммой R(ω) и I(ω) в де­картовых координатах на комплексной плоскости. В полярных координатах соответственно

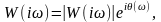(3.2.19)

где

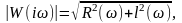(3.2.20)

(3.2.21)

Функции |W(iω)| и θ (ω) определяют изменение ам­плитуды и фазы колебаний на выходе по отношению к амплитуде и фазе колебаний на входе и называются соответственно амплитудной частотной (АЧХ) и фа­зовой частотной (ФЧХ) характеристиками.

Рассматривая W(iω) как вектор и варьируя ча­стоту входного сигнала ω от 0 до ∞, получим на ком­плексной плоскости кривую, описываемую концом этого вектора. Эта кривая называется годографом вектора комплексной частотной функции или ампли­тудно-фазовой частотной характеристикой (АФЧХ). Заметим, что W(i∞) = 0 (см. подглаву 3.2.1, свойство 1).

Широкое практическое применение нашли частот­ные характеристики, построенные в логарифмическом масштабе. Логарифмируя соотношение (3.2.19), полу­чим

In W (iω) = In |W( iω)| + iθ (ω). (3.2.22)

Зависимость L_m=20lg|W(iω)|=L_m(lgω) называется логарифмической амплитудно-частотной характеристи­кой (ЛАЧХ), a θ=θ(lgω) -логарифмической фазо-частотной характеристикой (ЛФЧХ).

ЛАЧХ и ЛФЧХ строятся в логарифмическом мас­штабе, по оси абсцисс откладывается десятичный ло­гарифм частоты. За единицу масштаба принимается декада - частотный интервал, соответствующий изме­нению частоты в 10 раз. По оси ординат при построе­нии ЛФЧХ фаза откладывается в радианах или угловых градусах. При построении же ЛАЧХ отклады­вают не величину L = lg|W(iω)|, а пропорциональ­ную ей величину L_m= 20lg|W(iω)| в децибелах. В табл. 3.1 приводятся значения L_m как функции |W(iω)|.

Таблица 3.1 - Значения L_m как функции |W (iω)|

|W (iω)|	0,01	0,1	1	1,12	1,26	1,41	1,8	3,6	10	100
Lm	-40	-20	0	1	2	3	5	10	20	40