Вопрос 27 Выпуклость функции, точки перегиба

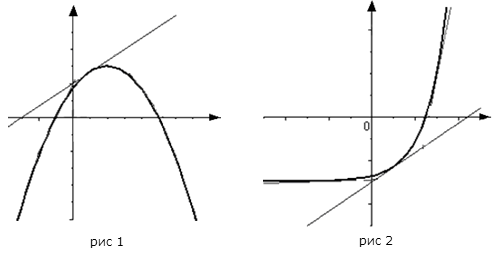
График функции , дифференцируемой на интервале , является на этом интервале выпуклым, если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым, если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Теоремы о выпуклости функции и точках перегиба

Теорема

(Об условиях выпуклости или вогнутости графика функции)

Пусть функция определена на интервале и имеет непрерывную, не равную нулю в точке вторую производную. Тогда, если всюду на интервале , то функция имеет вогнутость на этом интервале, если , то функция имеет выпуклость.Определение

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

Вопрос 28 Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке

Говорят, что функция , определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство .

Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Вопрос 30 Первообразная и неопределенный интеграл

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).Обозначение где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением. ойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. 2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то 4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

Вопрос 31

Вопрос 32

6. Метод подстановки (замена переменной интегрирования)

Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: а) где – монотонная, дифференцируемая функция; б) – новая переменная.В первом случае формула замены переменной имеет вид: . (6.1) Во втором случае: . (6.2) В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.

Вопрос 33 Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала). Свойства Если функция интегрируема по Риману на , то она ограничена на нем.

Вопрос 34   Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a, b], то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.).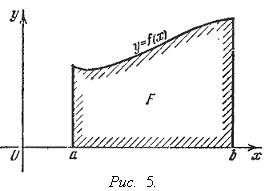

Вопрос 35 Определение. Разность F (b)– F (a) называется интегралом от функции f (x) на отрезке [ a ; b ] и обозначается так: = F (b)– F (a) – формула Ньютона-Лейбница.

Геометрический смысл интеграла.

Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b: .Вычисление площадей с помощью интеграла.

Вопрос 36 Дифференциальным уравнением называется уравнение, связывающее независимую переменную , искомую функцию и её производные , т. е. уравнение вида Если искомая функция есть функция одной независимой переменной , дифференциальное уравнение называется обыкновенным; например,Когда искомая функция есть функция двух и более независимых переменных, например, если , то уравнение виданазывается уравнением в частных производных. Здесь — неотрицательные целые числа, такие, что ; напримерДифференциальные уравнения – это соотношение вида F(x₁,x₂,x₃,..,y,y′,y′′,...y⁽ⁿ⁾) = 0, связывающее независимые переменные x₁,x₂,x₃,... функцию y этих независимых переменных и ее производные до n-го порядка. При этом функция F определена и достаточное число раз дифференцируема в некоторой области изменения своих аргументов.