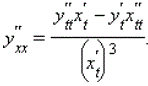ВОПРОС 1 Аксиомы стереометрии[править исходный текст] На каждой прямой и в каждой плоскости имеются по крайней мере две точки. В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что: любые две точки, принадлежащие разным множествам, разделены плоскостью α;любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

ВОПРОС 2 Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек (а || )Признак параллельности прямой и плоскости.Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.

Вопрос 3 Теорема. Если прямая параллельна плоскости, то она параллельна некоторой прямой на этой плоскости. ... Теореме можно дать другую, более удобную формулировку.Если прямая параллельна плоскости и содержится в другой плоскости, пересекающей первую, то она параллельна линии пересечения этих плоскостей.

Вопрос 4 Определение 2.5. Две плоскости называются параллельными , если они не имеют общих точек. Теорема 2.6. Признак параллельности плоскостей. Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны.

Вопрос5 Теоремы о параллельности прямых и плоскостей Если прямая параллельна какой-нибудь прямой , расположенной в плоскости , то она параллельна самой плоскости. Если плоскость проходит через прямую , параллельную другой плоскости , и пересекает эту плоскость, то линия пересечения параллельна первой прямой . Если две параллельные плоскости и пересекаются третьей плоскостью , то линии пересечения и параллельны. Если две пересекающиеся прямые и (рис. 3) одной плоскости соответственно параллельны двум прямым и другой плоскости, то эти плоскости параллельны.

Вопрос 6 ОпределениеПрямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения. Теорема 1ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.Доказательство.

Вопрос 7 Теорема О ТРЕХ ПЕРПЕНДИКУЛЯРАХ.Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Вопрос 8 БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВАФункция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.Примеры.

Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как (см. рис.).

Функция f(x) = tgx – бесконечно малая при x→0.

f(x) = ln (1+x)– бесконечно малая при x→0.

f(x) = 1/x– бесконечно малая при x→∞.

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Вопрос 9 Определение 1. Постоянное число А называется предел функции f(x) при x→a, если для всякой последовательности {x_n} значений аргумента, стремящейся к а, соответствующие им последовательности {f(x_n)} имеют один и тот же предел А. Теорема Лопита́ля (также правило Бернулли — Лопиталя^[1]) — метод нахождения пределов функций, раскрывающий неопределённости вида и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных

Вопрос 10 Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.Функция называется непрерывной справа в точке , если .Функция называется непрерывной слева в точке , если .Функция называется непрерывной в интервале , если она непрерывна в каждой точке этого интервала.Функция называется непрерывной на отрезке , если она является непрерывной в интервале , непрерывной справа в точке , то есть и непрерывной слева в точке , то есть .

Вопрос 11 Теорема 1. Сумма непрерывных функций есть функция непрерывная. Доказательство. Пусть функции и непрерывны в точке a. Тогда

Согласно свойству пределов функций существование пределов функций     и     гарантирует существование предела их суммы. При этом что и требовалось доказать. Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная. Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция.

Вопрос 12 Физический смысл производной.Если точка движется вдоль оси х и ее координата изменяется по закону  x(t), то мгновенная скорость точки: Определение: Производной функции f(x) (f'(x₀)) в точке x₀  называется число, к которому стремится разностное отношение , стремящемся к нулю.

Вопрос 14Производная суммы функций Теорема. Если функции u (x) и v (x) дифференцируемы, то их сумма w (x) = и (x) + v (x) также дифференцируема, причемw' (x) = и' (x) + v' (x)(Производная от суммы двух функций равна сумме производных от этих функций.)Доказательство.  Имеем:Δ w (x)  = w (x + Δ x) — w (x) = [и (x + Δ x) + v (x + Δ x)] — [и (x) + v (x)] = = [и (x + Δ x) — и (x)] +   [v (x + Δ x) — v (x)]. Поэтому

Вопрос 15 Формула

Производная частного равна производная числителя, умноженная на знаменатель, минус производная знаменателя, умноженная на числитель, и разность делится на знаменатель в квадрате.

Вопрос 16 Степенно-показательной функцией (или показательно-степенной, или функцией в степени функция) называется функция вида

Вопрос 17 Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• арксинус (обозначение: )

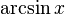• арккосинус (обозначение: )

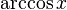• арктангенс (обозначени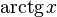е: ) в иностранной литературе ( )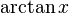

• арккотангенс (обозначени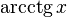е: ) в иностранной литературе (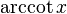 ) или ( )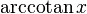

• арксеканс (обозначение: )

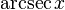• арккосеканс (обозначени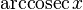е: ) в иностранной литературе ( )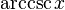

вопрос 18 Производные обратных тригонометрических функций Производные обратных тригонометрических функций можно вывести, используя теорему о производной обратной функции. Так, например, для функции  y = f (x) = arcsin x  обратной функцией является синус, т.е. x = φ (y) = sin y.  Тогда производная арксинуса равна:

Вопрос 19 Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Вопрос 20 Касательная и нормаль к кривойОпределение Касательная прямая - прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.Определение Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.

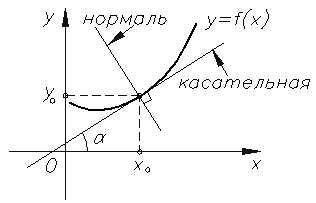
Вопрос 21 В соответствии с физическим смыслом производной, вторая производная – скорость изменения первой производной, т.е., согласно физическим терминам, ускорение изменения исходной функции. Вторая производная и ее физический смыслЕсли функция f’ дифференцируема, то ее производную называют второй производной от f и обозначают f”: f” = (f’)’ Вторая производная от параметрической функции x = x (t) и y = y (t) задается формулой: