6.9. Двоично-десятичный счетчик

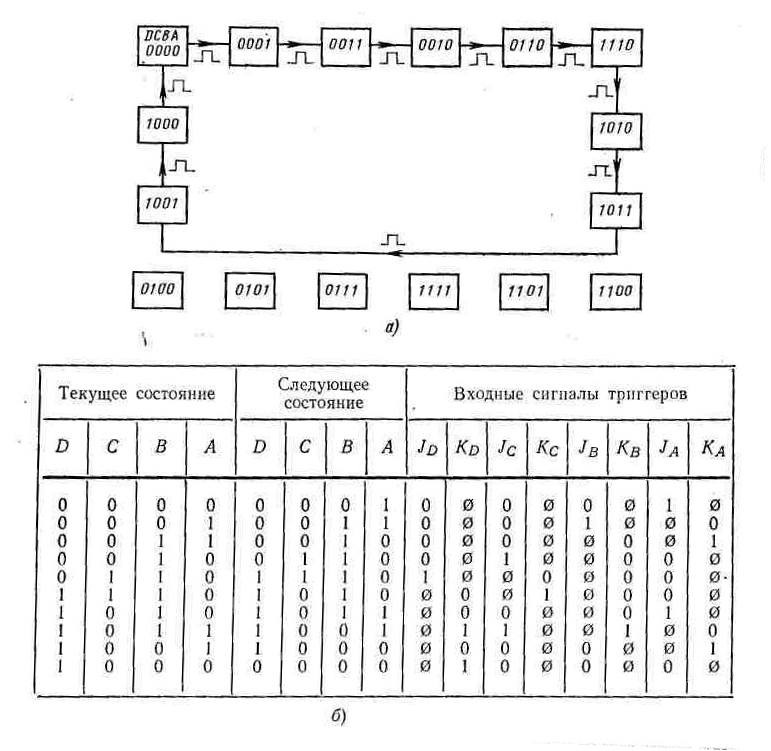
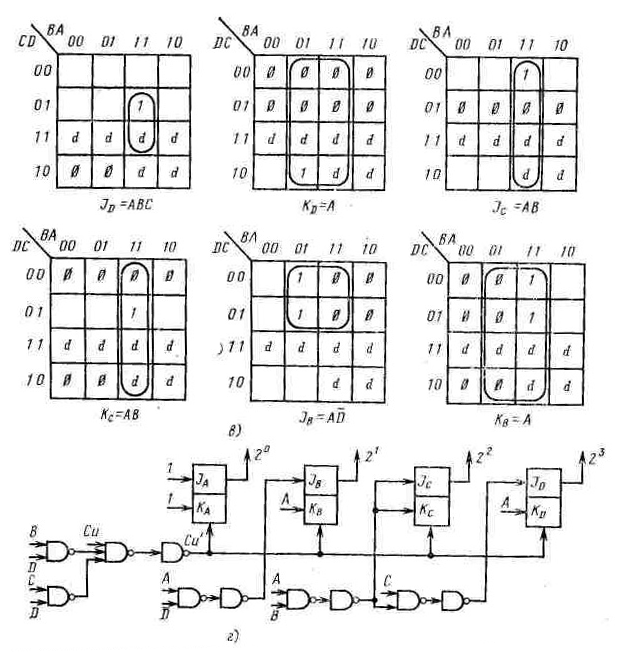
На рис. 6.7, а показана диаграмма состояний десятичного счет­чика, а на рис. 6.7, б - таблица состояний. В правой части таблицы приведены значения входных сигналов четырех триггеров. Для поиска этих значений были проанализированы те переходы, которые должны быть сделаны, а затем с помощью управляющей таблицы (см. рис. 6.1, б) определены соответствующие значения J и К входов триггеров.

На рис. 6,7, а приведены карты Карно для триггеров В, С и D. После упрощения для входов J и К были получены следующие выражения:

Просмотр столбцов J_A и К_А на рис. 6.7, б показывает, что все значения равны либо 0, либо 1. И так как неиспользуемые состояния могут также участвовать в процессе упрощения, то все ячейки карт Карно для J_A и К_А оказываются заполненными символами «0», «1» и «d». Следовательно,

J_A = К_А = 1.

Предположим, что из-за неисправности счетчик оказывается в одном из запрещенных состояний. Тогда необходимо предусмотреть специальные действия, блокирующие сигнал синхронизации и подающие сигнал тревоги. Для этого, как и раньше, может быть использована функция, описывающая неиспользуемые состояния f_U = BD + CD. На рис, 6.7, г показана схема счетчика. В этой схеме предусмотрена специальная цепь, подавляющая в случае необходимости импульсы синхронизации. Выражение, описывающее новый сигнал синхронизации, имеет вид

.

Если BD = 1 ила СD = 1, то Си' = 0 и синхроимпульсы подавляются.

Р ис. 6.7. Двоично-десятичный счетчик:

а - диаграмма состояние; б - таблица состояний; в - карты Карно; г - схема реализации

6.10. Двоично-десятичный счетчик обратного счета

И спользуя описанный выше метод, можно спроектировать двоично-десятичный счетчик обратного счета. Выражения для входных сигналов триггеров счетчика имеют вид

Рис. 6.8. Схема двоично-десятичного счетчика обратною счета

Схема счетчика приведена на рис. 6.8.

6.11. Десятичный счетчик, использующий код Грея

Рассмотрим переход из состояния 0001 в состояние 0010 для двоично-десятичного счетчика. Предположим, что триггер В изменяет свое состояние быстрее, чем триггер А. Последовательность, характеризующая изменения состояния триггеров, будет тогда иметь вид

D С В А

0 0 0 1

0 0 1 1 (промежуточное состояние).

0 0 1 0

Е

Рис. 6.9. Декодировщик, преобразу-ющий сигналы, поступающие с четырехразрядного двоичного счетчика, в десятичную форму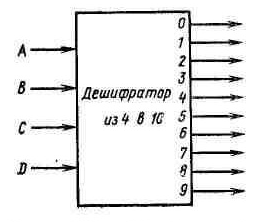

сли дешифратор, служащий для преобразования кода сигнала, передаваемого по четырем линиям, в один из десяти выходов (рис. 6.9) используется для формирования десятичного представления сигналов, которые поступают с выхода двоичного счетчика, то на выходной линии 3 будет появляться незапланированный выброс. Он может появиться в любой момент в такой двоичной счетчиковой схеме, где два и более триггеров используются для изменения состояния счетчика во время одного перехода. Эта трудность может быть преодолена, если применять для счета код Грея. Тогда во время каждого перехода только один триггер будет изменять свое состояние. Характерной особенностью кода Грея является то, что при переходе от любой кодовой комбинации к следующей за ней по порядку изменяется только одна цифра. При построении счетчика будем использовать код Грея соответствующий коду 2-4-2-1.

С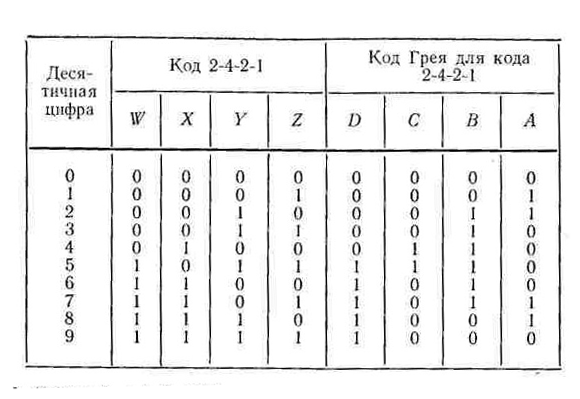 начала покажем, как из кода 2-4-2-1 может быть получен код Грея. На рис. 6.10 код 2-4-2-1 размещен в столбцах, помеченных буквами W, X, Y и Z. Для преобразования кода 2-4-2-1 в соответствующий ему код Грея можно использовать уравнения, полученные для преобразования двоичных чисел в код Грея (см. гл. 4).

Рис. 6.10. Двоичный код 2-4-2-1 и соответствующий ему код Грея

Применяя эти уравнения, получим конкретные значения для всех разрядов кода Грея. На рис. 6.10 код Грея расположен в столб­цах D, С, В и А.

Существует много различных четырехразрядных кодов Грея. На рис. 6.11, а показано, как изменяются позиции кодовых комбинаций на карте Карно при переходе от одной кодовой комбинации к другой для кода Грея с весовыми характеристиками разрядов 2-4-2-1. Следует заметить, что соседние кодовые комбинации занимают соседние ячейки карты Карно. Следовательно, для создания кода Грея, включающего десять комбинаций, достаточно на карте Карно начертить замкнутую кривую, которая проходит десять соседних ячеек. Одна из таких кривых показана на рис. 6.11, б. Соответствующий этой кривой код Грея приведен на рис. 6.11, в.

Р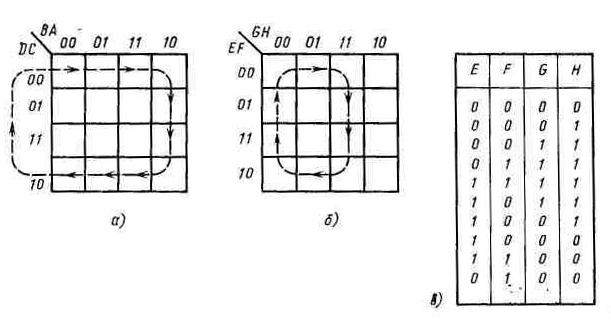 ис. 6.11. Коды Грея:

а – кривая на карте Карно, соответствующая коду Грея с весовыми характеристиками разрядов 2-4-2-1; б – задание кода Грея с помощью кривой, проведенной на карте Карно; в – кодовые комбинации для кода Грея, определенного в п. 6.

Вернемся к проектированию счетчика. На рис. 6.12, а показана диаграмма его состояний, а на рис. 6.12, б - таблица состояний. Эта таблица позволяет определить поведение каждого триггера в те моменты, когда счетчик изменяет свое состояние. Далее с помощью управляющей таблицы (см. рис. 6.1, б) можно получить значения входных сигналов триггеров. Они приведены в правой части таблицы состояний счетчика.

На рис. 6.12, б изображены восемь карт Карно, по одной для каждого входного сигнала. Как обычно, ячейки, соответствующие неиспользуемым состояниям, помечены символом «d», а остальные ячейки заполнены в строгом соответствии с таблицей (см. рис. 6.12, б).

Проведем упрощение описанным выше методом и в результате получим следующие выражения для входных сигналов триггеров:

На рис. 6.12, г приведена схема, реализующая этот счетчик.

Рис. 6.12. Счетчик, работающий в коде Грея с весовыми характеристиками разрядов 2.4-2-1:

а - диаграмма состояний; б - таблица состояний; в - карты Карно; г - реализация счетчика