6. Счетчики

6.1. Введение

Счетчиковые схемы являются простейшей формой последовательных схем. На практике счетчпковые схемы, так же как и другие последовательные схемы, формируют из элементов памяти, таких, как триггеры, и элементов комбинационной логики.

Все последовательные схемы подразделяются на два класса: синхронные (управляемые временем) н асинхронные (управляемые событиями). В синхронных схемах все изменения согласуются по времени с подачей синхронизирующих импульсов, а в схемах, управляемых событиями, все изменения состояния схемы регулируются определенными событиями, такими, как появление неисправностей.

Каждая счетчиковая схема относится к одному из описанных выше классов. Схемы, управляемые временем, называются синхронными счетчиками, а схемы, управляемые событиями, асинхронными счетчиками или счетчиками со сквозным переносом. Схему синхронного счетчика используют для подсчета импульсов синхронизации (тактовых импульсов); это число хранится в нескольких элементах памяти. Асинхронные счетчики применяют для определения количества нерегулярных событий, например, для определения числа людей, входящих в банк. Как и в случае синхронного счетчика, это число хранится в нескольких элементах памяти.

Счетчики являются основными компонентами цифровых систем и могут использоваться для целей управления и синхронизации. Они появляются в вычислительных системах и системах связи; они могут использоваться для деления частот. В одних случаях они могут быть чисто двоичными, в других ведут счет в коде Грея или в десятичном NBCD-коде.

6.2. Двоичный счетчик

Самым простым счетчиком является двоичный. Он может находиться в одном из двух состояний. Так как триггер также может находиться в одном из двух состояний, ясно, что двоичный счетчик можно реализовать с помощью единственного триггера.

О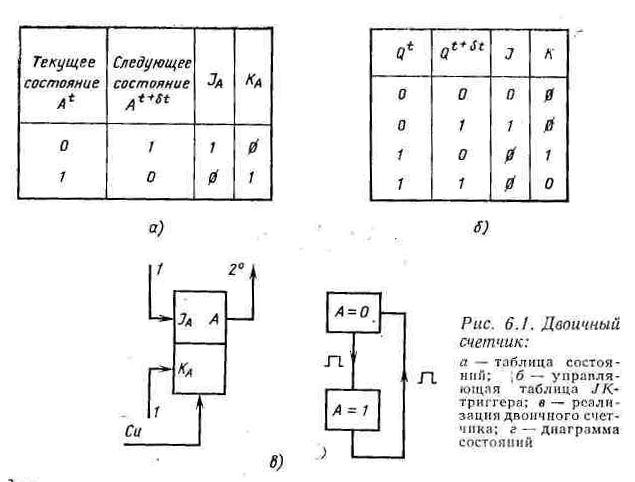 дин из методов проектирования счетчиков заключается в построении таблицы состояний, в первом столбце которой будут отражены текущие состояния счетчика, а во втором следующие за ними состояния. Такая таблица показана на рис. 6.1, а. Анализ таблицы позволяет установить соответствие между поведением счетчика и триггера. Если реализовать счетчик с помощью триггера, то переходы триггера должны осуществляться при переходе счетчика от текущего к следующему состоянию. Предположим, что для реализации счетчика выбран JK-триггер. Тогда состояния его входов J и К, требуемые для реализации переходов счетчика, можно взять на управляющей таблицы JК-триггера, приведенной на рис. 6.1, б. Поскольку значения входов J и K для второй и третьей строки равны либо , либо 1, то можно считать, что J_A = K_A = 1.

Схема счетчика приведена на рис. 6.1, в, а диаграмма состояний на рис. 6.1, г. В рассматриваемом случае диаграмма состояний является диаграммой как внешних, так и внутренних состоянии счетчика, поскольку, с одной стороны, А = 0 и А = 1 являются внутренними состояниями счетчика, а с другой стороны, значение А всегда присутствует на входе счетчика.

6.3. Счетчик по модулю 4

Счетчик по модулю 4 имеет четыре состояния и поэтому для его реализации достаточно двух триггеров. На рис. 6.2, а показана таблица состояний счетчика. Для того чтобы заполнить столбцы J_A, J_В, К_A и К_В,, сначала определяем те переходы, которые должны быть сделаны, а затем с помощью управляющей таблицы JK-триггера находим позволяющие осуществить эти переходы значения входов триггеров.

Р ис. 6.2. Счетчик по модулю 4:

а – таблица состояний; б – карты Карно; в - диаграмма состояний; г – реализация счетчика

Анализ J_A и К_А столбцов таблицы состояний показывает, что все их значения равны либо , либо 1. Следовательно, J_A = К_A = 1. Для определения значении J_В и К_В используем карту Карно, изображенную на рис. 6.2, б. После упрощений находим, что J_В = К_В = А. На рис. 6.2, в дана реализация счетчика, а на рис. 6.2, г показана его диаграмма состояний.