56. Средняя арифметическая форма индекса.

Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. Средний индекс должен быть тождественен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.

Арифметическая форма индекса используется для сводных индексов количественных показателей, а гармоническая форма индекса – для расчета сводных индексов качественных показателей.

Средний арифметический индекс объема продукции вычисляется:

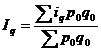, так как  .

Индекс Доу-Джонса (Dow Jones Industrial Average Index) определяется как средний арифметический индекс значений курсов акций, котирующихся на Нью-Йоркской фондовой бирже. Один сводный и три групповых индекса рассчитываются каждые полчаса, и ежедневно публикуется из значение на момент закрытия биржи.

Индекс Стэндарда и Пура (Standart and Poor's 500 Stock Index) – индекс, рассчитываемый по курсам акций 500 крупнейших компаний Нью-Йоркской фондовой биржи как средневзвешенный показатель, учитывающий общее количество выпущенных акций.

Индекс цены в средней арифметической форме:

Индекс себестоимости в средней арифметической форме:

В статистике широко известен индекс Струмилина - среднеарифметический индекс, который используется при анализе производительности труда.

Индекс Струмилина показывает во сколько раз возросла или уменьшилась производительность труда или сколько процентов составил рост или снижение производительности труда в среднем по всем единицам исследуемой совокупности.

57. Средняя гармоническая форма индекса.

Средняя гармоническая форма индексов.

Индекс цены в средней гармонической форме:

Индекс физического объема продукции в средней гармонической форме:

Индекс себестоимости в средней гармонической форме:

 

58. Индексы постоянного состава.

Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.

Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности. Задача определения влияния каждого фактора определяется с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.

Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции:

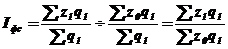
59. Индексы переменного состава.

Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.

Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности. Задача определения влияния каждого фактора определяется с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.

Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава себестоимости продукции:

.

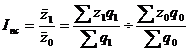Отражает изменение не только изменение индексируемой величины (в данном случае, себестоимости), но и структуры совокупности весов (объем).