50. Сущность индексов. Общие и индивидуальные индексы.

Индексы относятся к важнейшим обобщающим показателям. С их помощью производится анализ развития социально-экономических явлений в пространстве и времени, выявляется роль отдельных факторов в формировании важнейших экономических показателей.

Термин «индекс» имеет несколько значений: это показатель, указатель, опись, реестр, условное обозначение. В статистике индекс – это относительная величина, получаемая в результате:

1. сопоставления уровней социально-экономических явлений во времени (динамические индексы) или в пространстве (территориальные индексы);

2. сравнения фактических данных с эталонными (план, прогноз, норматив)

Индивидуальные индексы.

Индивидуальные индексы – получают в результате сравнения однотоварных явлений. Они вычисляются по конкретному товару отдельно. С их помощью можно охарактеризовать динамику отдельных элементов той или иной совокупности.

Все индивидуальные индексы, являясь показателями роста, показывают во сколько раз (или на сколько %) произошло изменение изучаемого показателя, характеризующего данный вид продукта/товара в отчетный период по сравнению с базисным.

Общие (агрегатные) индексы.

В отличие от индивидуальных индексов характеризуют динамику всего изучаемого явления, состоящего из разнородных единиц.

В индексной теории изложены 2 концепции их построения:

• синтетическая – предполагает с помощью индексного метода соединение в целое разнородных единиц статистической совокупности и их последующую характеристику. Пример: предприятие выпускает разнородную продукцию, физический объем ее выпуска нельзя суммировать. Для определения общего объема выпуска методология индексов предусматривает, прежде всего, приведение разнотоварных явлений к соизмеримому виду;

• аналитическая – предполагает с помощью индексного метода выявление и измерение влияние факторов на изучаемое явление.

Общий индекс может быть построен 2 способами:

• как агрегатный (основной);

• как средний из индивидуальных.

В числителе и знаменателе агрегатного индекса находится сумма произведений двух показателей, один из которых меняется, т.е. выступает в роли индексированной величины, а второй остается неизменным, т.е. выступает в роли соизмерителя (весы).

1. Общий индекс физического объема (товарооборота):

Позволяет сопоставить изменение в объеме многих видов несоизмеримых между собой товаров.

Для расчета необходимо преодолеть несуммируемость количества этих товаров. Для этого надо подобрать соизмеритель (вес), который позволит представить продукцию за каждый из периодов в сопоставимом виде. Таким соизмерителем является цена!

Показывает во сколько раз (или на сколько %) изменилось количество продаваемых товаров в отчетном периоде по сравнению с базисным.

2. Общий индекс цен:

Показывает во сколько раз (или на сколько %) изменились цены реализации товаров в отчетном периоде по сравнению с базисным.

3. Общий индекс товарооборота в фактических (действительных) ценах:

В данном индексе цена и количество одновременно являются как индексируемыми величинами, так и соизмерителями.

Существует противоположная форма построения этих индексов (есть противоположные правила выбора весов).

Пааше (весы за отчетный период)

Ласпейрес (весы за базисный период)

 

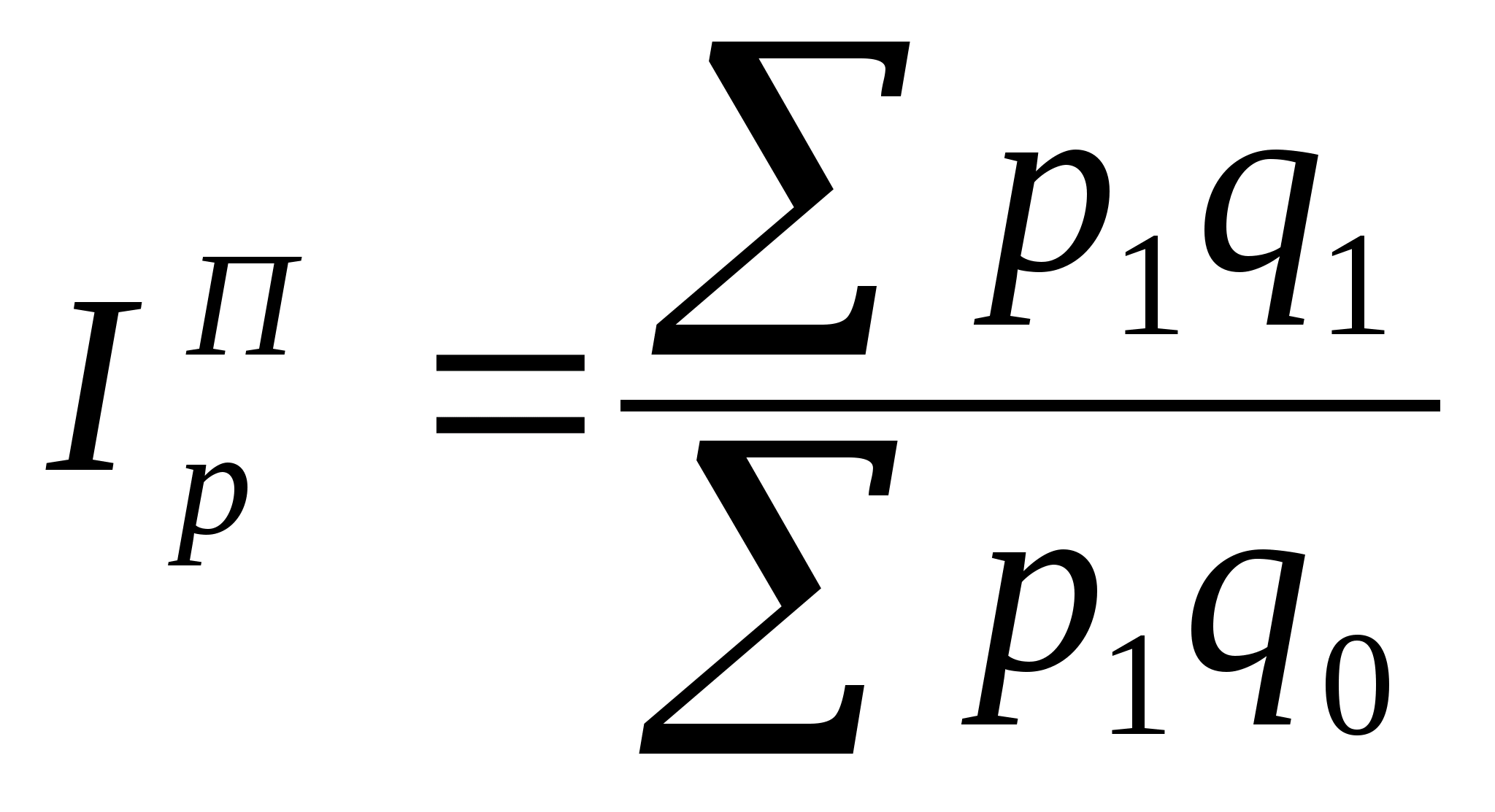
Фишер   – «идеальная формула» Фишера (по сравнению геом.)