41. Условия применения и ограничения корреляционно-регрессионного метода.
Первое условие (общее условие всякого статистического исследования) – наличие данных по достаточно большой совокупности явлений. По отдельным явлениям можно получить совершенно превратное представление о связи признаков, ибо в каждом отдельном явлении значения признаков кроме закономерной составляющей имеют случайное отклонение.
Второе условие – это условие, обеспечивающее надежное выражение закономерности в средней величине. Кроме уже указанного большого числа единиц совокупности для этого необходима достаточно качественная однородность совокупности. Нарушение этого уровня может извратить параметры корреляции.
Третье условие – необходимость подчинения распределения совокупности по результативному и факторным признакам нормальному закону распределения вероятностей. Это условие связано с применением метода наименьших квадратов при расчете параметров корреляции: только при нормальном распределении метод наименьших кадров дает оценку параметров, отвечающую принципам максимального правдоподобия.
42. Коэффициент корреляции рангов.
Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом.
Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирмэном и М. Кендэлом.
Коэффициент корреляции рангов Спирмэна (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле
где d = Nx - Ny , т.е. разность рангов каждой пары значений х и у; n - число наблюдений.
Ранговый
коэффициент корреляции Кендэла (
)
можно определить по формуле
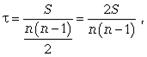где
S = P + Q.
43. Понятие о стохастических и функциональных связях.
Если с изменением значения одной из переменных вторая изменяется строго определенным образом, т.е. значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональной.
Нередко говорят о строгом соответствии лишь одного значения второй из переменных каждому значению первой из них, но это неверно. Например, связь между у и х является строго функциональной, если , но значению х = 4 соответствует не одно, а два значения: у1 = +2; у2 = - 2. Уравнения более высоких степеней могут иметь несколько корней, связь, разумеется, остается функциональной.
Функциональная связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более. В реальной природе (и тем более в обществе) таких связей нет; они являются лишь абстракциями, полезными и необходимыми при анализе явлений, но упрощающими реальность. Функциональная зависимость данной величины у от многих факторов х1, х2, ..., хn возможна только в том случае, если величина y всегда зависит только от перечисленного набора факторов x1, х2 ..., хk и ни от чего более. Между тем все явления и процессы безграничного реального мира связаны между собой, и нет такого конечного числа переменных k, которые абсолютно полно определяли бы собою зависимую величину y. Следовательно, множественная функциональная зависимость переменных есть тоже абстракция, упрощающая реальность.
Стохастически детерминированная связь не имеет ограничений и условий, присущих функциональной связи. Если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону - связь является статистической. Иными словами, при статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной.
В настоящее время наука не знает более широкого определения связи. Все связи, которые могут быть измерены и выражены численно, подходят под определение «статистические связи», в том числе и функциональные. Последние представляют собой частный случай статистических связей, когда значениям одной переменной соответствуют «распределения» значений второй, состоящие из одного или нескольких значений и имеющие вероятность, равную ' единице. Конечно, качественное различие действительно вероятностных распределений и отдельных значений, имеющих вероятность единицы (достоверных), настолько велико, что хотя функциональные связи и подходят в широком смысле под определение статистической связи, все же с полным основанием можно говорить о двух типах связей.