37. Виды трендовых моделей.

1. Линейная модель

2. Экспоненциальная модель

3. Логистическая модель

4. Кластерная модель

38. Статистическое изучение сезонных колебаний.

В статистике периодические колебания, которые имеют определенный и постоян­ный период, равный годовому промежутку, носят название сезонных колебаний, или сезонных волн, а динамический ряд в этом случае на­зывают тренд-сезонным, или просто сезонным рядом динамики.

Сезонные колебания характеризуются специальными показателя­ми, которые называются индексами сезонности (Is). Совокупность этих показателей отражает сезонную волну.

При использовании способа аналитического выравнивания  алгоритм вычислений индексов сезонности следующий:

·   по соответствующему полиному вычисляют для каждого месяца (квартала) выравненные уровни намомент времени (t);

·   определяют отношения фактических месячных (квартальных данных (у) ксоответствую-щим выравненным данным (уt) в процентах;  Ii=(yi:yt)*100;

·  находят средние арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах; Ii=(I1+I2+I3+…+In):n, n – число одноименных периодов.

В общем виде формулу расчета индекса сезонности данным спо­собом можно записать так:

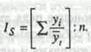
39. Понятие о статистической и корреляционной связи.

Исследователя нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, могут ли учащиеся с высоким уровнем тревожности демонстрировать стабильные академичес­кие достижения, или связана ли продолжительность работы учителя в школе с размером его заработной платы. Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь — это согласованное изме­нение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью дру­гого.

Известно, например, что в среднем между ростом людей и их весом наблюдается положительная связь, и такая, что чем боль­ше рост, тем больше вес человека. Однако из этого правила име­ются исключения, когда относительно низкие люди имеют из­быточный вес, и, наоборот, астеники, при высоком росте име­ют малый вес. Причиной подобных исключений является то, что каждый биологический, физиологический или психологический признак определяется воздействием многих факторов: средовых, генетических, социальных, экологических и т.д.

Корреляционные связи — это вероятностные изменения, которые можно изучать только на представительных выборках методами математической статисти­ки. «Оба термина, — пишет Е.В. Сидоренко, — корреляционная связь и корреляционная зависимость — часто используются как синони­мы. Зависимость подразумевает влияние, связь — любые согласован­ные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого.

Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (ли­нейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимо­сти полученных коэффициентов корреляции.

Статистическая связь может быть представлена уравнением следующего вида:

У, = f (X,) + S»

где у2 - расчётное значение результативного признака.

f (xt)- часть значения результативного признака, сформировавшаяся под воздействием учтённых факторов.

st - часть значения результативного признака, возникающая вследствие действия неконтролируемых факторов или ошибок измерения.

Примером статистической связи может служить зависимость себестоимости единицы продукции от уровня производительности труда: чем выше производительность труда, тем ниже себестоимость. Но на себестоимость единицы продукции помимо производительности труда влияют и другие факторы: стоимость сырья, материалов, топлива, общепроизводственные и общехозяйственные расходы и т.д. Поэтому нельзя утверждать, что изменение производительности труда на 5% (повышение) приведет к аналогичному снижению себестоимости. Может наблюдаться и обратная картина, если на себестоимость будут влиять в большей степени другие факторы, - например, резко возрастут цены на сырье и материалы.

Любую статистическую связь можно представить в виде набора локальных распределений результативного признака при фиксированных значениях факторного:

X1: Уи,У1,2...Уи ... У 1,m

X2 : У 2,1, У 2,2 ...У 2,j ... У 2,m

Xn УП,1, УП,2... УП,j ... Уn,m ,

где i = 1, n, j = 1, m .