Вопрос 42: Барометрическая формула. Распределение Больцмана.

Атмосферное давление убывает с высотой. Найдем зависимость этого давления от высоты . Давление на высоте h обусловлено весом столба возду-ха, расположенного выше h. С увеличением высоты давление падает. Убыль давления  dp при подъеме на dh равна весу воздуха, заключенного в столбе

высотой dh

		 dp gdh ,	(2.37)
где 	P	– плотность воздуха, выраженная из	уравнения Менделеева-
	RT

Клапейрона. Подставив это в (2.37), получаем дифференциальное уравнение:

	dp		g	dh .	(2.38)
	p		RT
Интегрируем (2.38) с дополнительным условием					p(0)  p0 – давление

на нулевой высоте (на уровне моря). Получаем:

		gh 	(2.39)
p  p0 exp		 .
		RT 

Выражение (2.39) называется барометрической формулой. Оно верно только для изотермической атмосферы. В реальной атмосфере температура изменяется с высотой. Однако, по шкале Кельвина относительное ее измене-ние не очень велико. Поэтому формула (2.39) достаточно хорошо выполняет-ся. Измеряя давление воздуха в атмосфере, можно найти высоту расположе-ния точки над уровнем моря. Прибор, предназначенный для этого, называет-ся альтиметром.

Учтем в (2.39) следующие соотношения: ^_R  ^m_k , p  nkT , p₀  n₀ kT ,

тогда:

		mgh 
n  n0 exp			.	(2.40)
		kT 

В (2.40) n и n₀ – концентрация молекул на высотах h и 0. Формула (2.40) от-

ражает противоборство двух факторов – потенциальной и тепловой энергии частиц. Увеличение m приводит к группировке частиц у поверхности h  0 , увеличение же Т приводит к обратному процессу рассеяния частиц по высо-те. Поскольку потенциальная энергия частицы E_п  mgh , то формулу (2.40)

можно записать в виде:

		E					E	
n  n0 exp			п	 или	dN xyz  n0 exp			п	dxdydz .	(2.41)
		kT 					kT 
Формула (2.41) выражает количество частиц с энергией Eп , попавших в объ-
ем dxdydz . Обе формулы (2.41)					соответствуют распределению Больцмана

молекул газа по их потенциальной энергии, в качестве которой может высту-пать не только энергия в поле тяжести, но и любая другая.

Распределения Максвелла и Больцмана имеют схожий вид. В первом определяющую роль играет кинетическая энергия молекул, во втором – по-тенциальная. Оба их можно объединить в одно распределение Максвелла-Больцмана:

Слева в выражении (2.42) стоит число молекул, попадающих в объем коор-динатного пространства dxdydz и скоростного пространства dv_x dv_y dv_z , а

справа – в виде сомножителя эти объемы.

Распределение Максвелла-Больцмана можно представить иначе, если записать его для числа молекул в единице объема, находящихся в потенци-альном поле с энергией E_п и имеющих скорость в интервале от v до v  dv

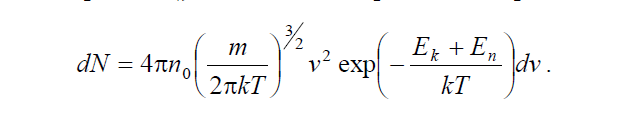
Если полная энергия молекулы может принимать только дискретные значения E₁ , E₂ , …, E_n , то распределение Больцмана для i-го состояния

и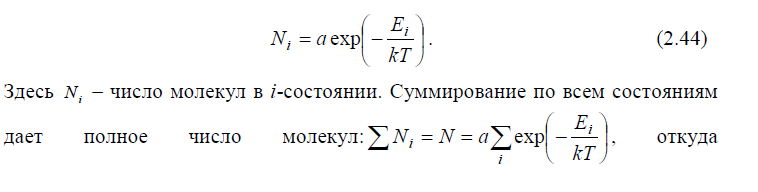 меет вид: