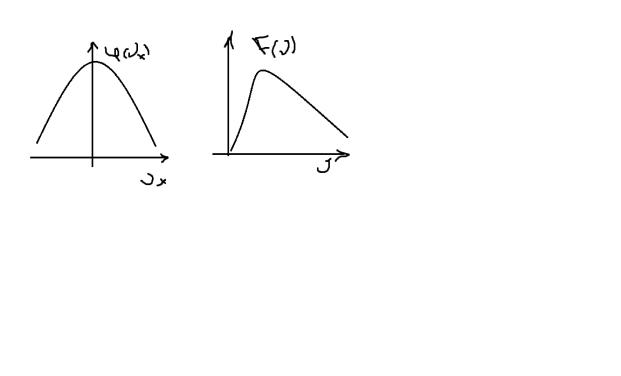Вопрос 36

Термодинамической системой наз-ся совокупность микроскопических объектов, обменивающихся энергией в форме работы и теплоты как друг с другом , так и с внешней средой. Терм-я система наз-ся замкнутой или изолированной, если она не может обмениваться с внешней средой ни энергией, ни веществом. Терм-я система наз-ся изолированной в тепловом отношении или адиабатной, если отсутствует теплообмен между ней и окружающей средой. Терм-я система наз-ся изолированной в механическом отношении , если она способна обмениваться с внешней средой энергией только путём теплообмена, без совершения механической работы. Терм-я система наз-ся открытой, если она обменивается с внешней средой и веществом и энергией. Терм-я система наз-ся закрытой, если она обменивается веществом с внешней средой. Гомогенной наз-ся Терм-я система, внутри которой нет поверхности раздела, отделяющих друг от друга макроскопические части системы. В противном случае она наз-ся гетерогенной. Фазой наз-ся гомогенная часть гетерогенной системы. Термодин-ми параметрами (параметрами состояния) наз-ся физ-е величины, характеризующие состояние термодинамической ситемы. Термодин-е параметры, значения которых пропорц-ны кол-ву вещ-ва, наз-т экстенсивными(масса, объём) ; значения же которых не зависят от кол-ва вещ-ва – интенсивными(температура, намагниченность).Внешними параметрами системы наз-ся физические величины, зависящие от положения и свойств тел, которые явл-ся внешними по отношению к данной системе.(например, для газа –объём). Внутренними параметрами системы наз-ся физ-е величины, зависящие как от положения внешних тел, так и от состояния движения частиц , образующих систему. Равновесными наз-ся состояния термодин-й системы , характеризующееся при неизменных внешних условиях постоянных параметров системы и отсутствием в в системе различных потоков. Термодин-м процессом наз-ся всякое изменение состояний термодин-й системы , при котором изменяется хотябы один её параметр. Термодинам-й процесс наз-ся равновесным, если система проходит непрерывный ряд термодинм-ки равновесных состояний.

Вопрос 37

В молекулярной физике используют модель идеального газа, в которой считают, что молекулы большую часть времени нах-ся в состоянии свободного движения, при этом их потенциальная энергия равна нулю, а полная энергия газа равна сумме кинетических энергий молекул.Уравнение связывающие между собой давление газа, его объём и температуру, наз-ся термическим ур-ем состояния: . Таким ур-ем описывается состояние простой ситемы, у которой имеется один внешний параметр V, а внешних полей нет. Для идеального газа используется ур-е состояния: или Из ур-я можно получить ур-я некоторых процессов, пологая равной константе давление, температуру, объём. Эти процессы наз-ся соот-но изобарный, изохорный, изотермический. Для идеального газа справедлив закон Дальтона: давление смеси газов равно сумме парциальных давлений каждого газа. Вопрос 38

Найдём давление, оказываемое молекулами идеального газа на стенку сосуда, в котором он находится. Считаем удары молекул абсолютно упругими, т.е. угол падения Θ равен углу отражения от стенки.Импульс, сообщаемый одной молекуле массы m , движущейся к стенке со скоростью v, равен: 2mvcosΘ. Столкнулся со стенкой площади ΔS за время Δt молекулы, нах-ся от стенки по направлению движения по направлению движению на расстоянии vΔt. Число таких молекул, движущихся в пределах телесного угла , равно их числу, попавшему в объём косого цилиндра : , где вт(м)- число молекул в единице объёма, имеющих скорость в пределах от v до v+dv. Импульс, переданный стенке всеми такими молекулами: . Интегрируя в сферической системе координат это выражение по направлениям полупространства , , имеем: . Давление, с учётом второго закона Ньютона, записанного в импульсной форме, определяется соотношением: . Введём понятие средней квадратичной скорости как: . Значения интегралов (1) по соответственно равный 1/3 и 2π. С учётом всего сказанного: . Если ввести среднюю кинетическую энергию молекул , то (2) примет вид:

Вопрос 39.Средняя энергия молекул . Термодинамическая температура есть величена пропорциональный средней энергии поступательного движения молекл. По причине изотропности св-в газа (одинаковости св-в в разных направлениях) , где обазначено среднее значение квадрата одной компоненты скорости: . Числом степеней свободы механической системы наз-ся число независимых параметров, полностью определяющих положение системы в пространстве.(для одноатомной молекулы число степенй свободы равно i=3) На каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия равная kT/2. На всю молекулу, таким образом, приходится энергия ikT/2, а на моль идеального газа:

Вопрос 40 (1), (2) Выражений (1)и(2) представляют распределение молекул газа по скоростям, принадлежащие Максвелу. При увеличении температуры максимум кривой F(v) смещается в сторону больших v, так что площадь под кривой остаётся при любой температуре равной 1.