Вопрос 50: Третий закон термодинамики.

В любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к абсолютному нулю, изменение энтропии S стремится к нулю:

lim S  0 .	(2.83)
T 0

Эта теорема, установленная Нернстом, называется третьим законом термо-динамики.

В формулировке Планка он записывается так. При стремлении термо-

динамической температуры тел к нулю их энтропия обращается в нуль. Это позволяет константу в (2.72) при интегрировании по температуре от 0 до T считать равной нулю. При T  0 теплоемкости C_P и C_V , коэффициент объ-

емного расширения ^V _T также стремятся к нулю. Из теоремы Нернста

следует, что невозможен такой термодинамический процесс, который приво-дил бы к охлаждению системы до температуры T  0 .

10.10 Термодинамические потенциалы.

Широкое распространение в термодинамике получил метод исследова-ния, развитый Гиббсом. Он основан на использовании так называемых тер-модинамических потенциалов – таких функций независимых макроскопиче-ских термодинамических параметров, которые полностью задают термодинамическое состояние системы. Если
известно аналитическое выражение любо-
			H
го термодинамического потенциала через
независимые параметры системы, то мож-
но в явной форме определить все ее тер-
модинамические величины. Все термоди-		TS
намические потенциалы аддитивны, кро-
			G
ме того, их дифференциалы являются
полными, значит, термодинамические по-
тенциалы сами являются функциями со-			Рис. 2.12
стояния системы. В простых системах ис-
пользуют следующие термодинамические потенциалы:
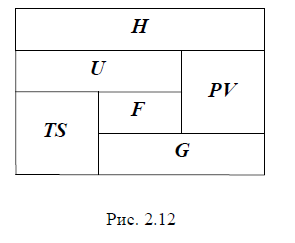
внутренняя энергия U;
свободная энергия (энергия Гельмгольца)
F  U  TS ;		(2.84)
энтальпия (тепловая функция)
H  U  PV ;		(2.85)
энергия Гиббса (потенциал Гиббса)
G  U  PV  TS ;		(2.86)

Соотношение между ними удобно представить в графическом виде (рис. 2.12).

1. Для дифференциала внутренней энергии в обратимых процессах справедливо соотношение, полученное из (2.82):

dU  TdS  pdV ,

(2.87)

из чего следует, что независимыми переменными для U являются S и V.

• В изохорном процессе dU Q_V .

• В адиабатическом процессе dU A_S .

	U 		U 
● T 		, p 	 .
	S V		V S

2. Для дифференциала свободной энергии с учетом (2.87) справедливо

соотношение

dF SdT  pdV ,

(2.88)

из чего следует, что независимыми переменными для F являются T и V. ● В изотермическом процессе dF A_T .

	F 		F 
● S 		; p 	 .
	T V		V T

● В необратимом процессе при постоянных T и V, разделив (2.82) на изменение времени dt и перегруппировав слагаемые, получим:

dU  TS  _ dF _{ 0 .} dt dt

В таком процессе свободная энергия уменьшается и достигает минимума в состоянии равновесия.

3. Для дифференциала энтальпии с учетом (2.87) справедливо соот-ношение:

dH  TdS  Vdp ,

(2.89)

из чего следует, что независимыми переменными для H являются S и p.: ● В изобарном процессе dH Q_P .

	H 		H 
● T 		; V 	 .
S P			
			pS

4. Для дифференциала энергии Гиббса с учетом (2.87) справедливо соотношение:

dG  Vdp  SdT ,

(2.90)

из чего следует, что независимыми переменными для G являются p и T.

	G 		G 
● V 		; S 	 .
		T P
	pT

● В необратимом процессе при постоянных p и T аналогично получа-

ем:

dU  PV  TS  _ dG _{ 0 .} dt dt

В таком процессе энергия Гиббса уменьшается и достигает минимума в со-стоянии равновесия.

51. Термодинамические потенциалы. Широкое распространение в термодинамике получил метод исследования, развитый Гиббсом. Он основан на использовании так называемых термодинамических потенциалов – таких функций независимых макроскопических термодинамических параметров, которые полностью задают термодинамическое состояние системы. Если известно аналитическое выражение любого термодинамического потенциала через

независимые параметры системы, то можно в явной форме определить все ее термодинамические величины. Все термодинамические потенциалы аддитивны, кроме того, их дифференциалы являются полными, значит, термодинамические потенциалы сами являются функциями состояния системы. В простых системах используют следующие термодинамические потенциалы: внутренняя энергия U; свободная энергия (энергия Гельмгольца): F=U-TS(1), энтальпия (тепловая функция)H =U + PV (2); энергия Гиббса (потенциал Гиббса)G =U + PV - TS (3). ). 1. Для дифференциала внутренней энергии в обратимых процессах справедливо соотношение, dU = TdS – pdV, из чего следует, что независимыми переменными для U являются S.● В изохорном процессе dU= . ● В адиабатическом процессе dU=- . ●T= _V, p= _S. 2. Для дифференциала свободной энергии справедливо соотношениеdF = -SdT - pdV,из чего следует,что для независимыми переменными для F явл-ся для T и V. ● В изотермическом процессе ●S=-( )_V;p=-( )_T. ● В необратимом процессе при постоянных T и V получим: . В таком процессе свободная энергия уменьшается и достигает минимума в cостоянии равновесия. 3. Для дифференциала энтальпии с учетом справедливо соотношение: dH = TdS + Vdp ,из чего следует, что независимыми переменными для H являются S и p.: ● В изобарном процессе:dH= . ●T=( )_p;V=( )_S. 4. Для дифференциала энергии Гиббса с учетом справедливо соотношение: dG =Vdp - SdT , из чего следует, что независимыми переменными для G являются p и T. ●V=( )_r;S=-( )_p. ● В необратимом процессе при постоянных p и T аналогично получаем:

d(U+pV-TS)/dt=dG/dt≤0. В таком процессе энергия Гиббса уменьшается и достигает минимума в состоянии равновесия.

52.Межмолекулярное взаимодействие. Уравнение состояния реальных газов. Молекулы в реальном газе взаимодействуют между собой. Это взаимодействие начинает проявляться на расстоянии порядка 10^-9 м в виде притяжения. На расстоянии порядка 10^-10 м притяжение сменяется взаимным отталкиваем. Сила притяжения и отталкивания зависят от расстояния между ними по степенному закону F , где n 13 для отталкивания и n 7 для притяжения. Газообразному состоянию соответствует соотношение kT >W₀ , жидкому kT ≤W₀ , твердому

kT <W₀ . Идеальный газ является моделью, которая хорошо описывает состояние газа в пределе высоких температур и низких давлений. В остальных случаях имеются более или менее значительные отклонения. Во многих случаях уравнение состояния идеального газа Менделеева-Клапейрона является непригодным. Для описания реальных газов были предложены соответствующие уравнения состояния.

Уравнение состояния Ван-дер-Ваальса для одного моля газа имеет вид:

(p+ )(Vm-b)=RT (1)Ван-дер-Ваальс

где р – давление, Vm– молярный объем, Т – термодинамическая температура.

Константа b определяет суммарный объем, занятый всеми молекулами газа вследствие конечности их размеров, а поправка a/V²– некоторое «внутреннее» давление, обусловленное взаимным притяжением молекул. Для ν молей уравнение (1) имеет вид:

(p+ )( – b)=RT

Более точными уравнениями состояния реальных газов являются:

● Первое и второе уравнения Дитеречи:

P(Vm-b)=Rt exp(- )(1): (p+ )(Vm-b)=RT(2) (1) и (2)-ур-е Дитеречи.

● Ур-е Бертло (p+ )(Vm-b)=RT

●Вириальная форма (1+ + + + …),где B, C, D – функции температуры, называющиеся вириальными коэффициентами.

55.Фазовый переход 1-го рода. Фазой называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза — вода; газообразная фаза — смесь воздуха с водяными парами. Если в воду бросить кусочки льда, то эта система станет трехфазной, в кото­рой лед является твердой фазой. Часто понятие «фаза» употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим свойствам, составу и строению (лед, например, встречается в пяти различных модификациях — фазах). Переход вещества из одной фазы в другую — фазовый переход — всегда связан с качественными изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую). Различают фазовые переходы двух родов. Фазовый переход I рода (например, плавление, кристаллизация и т. д.) сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода. Фазовые переходы I рода харак­теризуются постоянством температуры, изменениями энтропии и объема. Объяснение этому можно дать следующим образом. Например, при плавлении телу нужно сооб­щить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решетки. Подводимая при плавлении теплота идет не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. В подобных переходах — из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние — степень беспорядка увеличивается, т. е., согласно второму началу термодинамики, этот процесс связан с возрастанием энтропии систе­мы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет. = -уравнение Клайперона-Клаузиуса.

56.Фазовый переход 2-го рода. Фазой называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза — вода; газообразная фаза — смесь воздуха с водяными парами. Если в воду бросить кусочки льда, то эта система станет трехфазной, в кото­рой лед является твердой фазой. Часто понятие «фаза» употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим свойствам, составу и строению (лед, например, встречается в пяти различных модификациях — фазах). Переход вещества из одной фазы в другую — фазовый переход — всегда связан с качественными изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую). Фазовые переходы, не связанные с поглощением или выделением теплоты и измене­нием объема, называются фазовыми переходами II рода. Эти переходы характеризуют­ся постоянством объема и энтропии, но скачкообразным изменением теплоемкости. Общая трактовка фазовых переходов II рода предложена академиком Л. Д. Ландау (1908—1968). Согласно этой трактовке, фазовые переходы II рода связаны с изменени­ем симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода. Примерами фазовых переходов II рода являют­ся: переход ферромагнитных веществ (железа, никеля) при определенных давлении в температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое скачкооб­разным уменьшением электрического сопротивления до нуля; превращение обыкновен­ного жидкого гелия (гелия I) при Т=2,9 К в другую жидкую модификацию (гелий II), обладающую свойствами сверхтекучести. ΔCp= - T( )^2*Δ( )T; Δ( )p= - *Δ( )Tуравнение Эренфеста.