Вопрос 48: Циклические процессы. Теорема Карно.

Циклическим называется термодинамический процесс, по окончании которого система возвращается в исходное состояние. На любой диаграмме такому процессу соответствует замкнутая линия.

Тело, совершающее круговой процесс (цикл) и обменивающееся энерги-ей с другими телами, называется рабочим телом.

	p	a		T	1		2	T	A1	A2
				T1
1
		A	2			A			A
										A3
		b	V	T2	4	3	S	A4	Q	S
	V1		V2		S1		S2	S1		S2
		Рис. 2.5				Рис. 2.6			Рис. 2.7

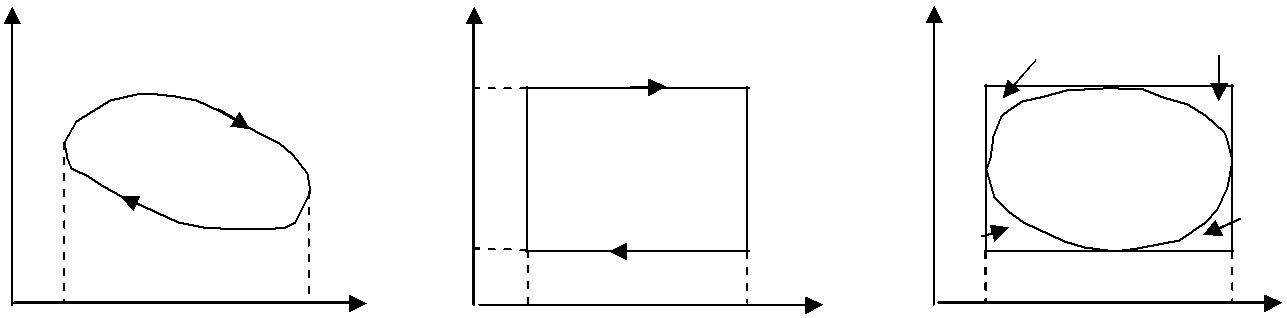
На диаграмме P, V процесс расширения газа показан кривой 1а2 (рис. 2.5). При этом газ получает от нагревателя количество теплоты Q₁. Сжатие газа происходит по кривой 2b1, здесь он отдает холодильнику количество те-плоты Q₂. Работа газа A  Q₁  Q₂ . Эта величина положительна, если ход

цикла происходит по часовой стрелке (прямой цикл). В обратном цикле с об-ходом против часовой стрелки работа отрицательна.

Коэффициентом полезного действия (кпд) называется величина

	A		Q1  Q2	1 	Q2	.	(2.77)
	Q		Q
					Q
	1	1		1

Цикл, состоящий из двух изотерм и двух адиабат, называется циклом Карно. На диаграмме Т, S он представляется прямоугольником (рис. 2.6). На отрезке 1-2 тело получает количество теплоты T₁ (S₂  S₁ ) , на отрезке 3-4 –

отдает количество теплоты T₂ (S₂  S₁ ) . Работа равна площади треугольника

A  Q1  Q2 . Легко найти кпд цикла Карно:
K	 1	T2 (S2  S1 )	 1	T2		T1  T2	.	(2.78)
		T1 (S2  S1 )		T1
						T1

Покажем, что цикл Карно имеет максимальный кпд по сравнению с любым другим циклом, работающим при тех же температурах T₁ и T₂ нагре-вателя и холодильника. Как видно из рис. 2.7, одновременно изображающего

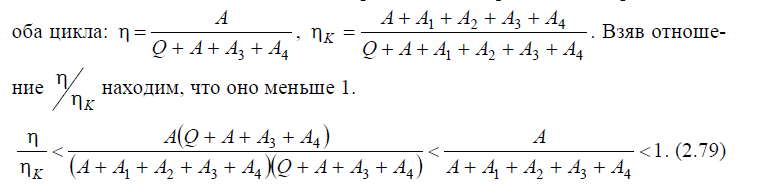
Т ем самым мы покали, что справедлива теорема, доказанная Карно. Термический кпд цикла Карно не зависит от природы рабочего тела и опре-деляется только температурами нагревателя и холодильника. Кроме того, кпд любого обратимого цикла η не может превосходить кпд цикла Карно, прове-денного между экстремальными температурами рабочего тела в рассматри-ваемом цикле. Можно также показать, что кпд любого необратимого цикла также меньше кпд соответствующего цикла Карно.