Вопрос 44: Теплоемкость

Теплоемкостью тела называется величина, равная количеству тепло-ты, которое нужно сообщить телу, чтобы повысить его температуру на один Кельвин.

Стела		Q		.	(2.49)
		dT
Удельной теплоемкостью называется теплоемкость единицы массы вещества
c 	Q		.		(2.50)
	mdT

Молярной теплоемкостью называется теплоемкость одного моля вещества

С 	Q	c	(2.51)
	dT

Поскольку Q определяется процессом теплопередачи, теплоемкость

тоже различна для различных процессов. Наиболее важными, получившими наибольшее применение, являются молярные теплоемкости при постоянных объеме и давлении С_V и С_P (изохорная и изобарная молярные теплоемко-

сти).

В случае изохорного процесса A  0 и Q  dU . Тогда

C 	dU M	,	(2.52)
V	dT

где U _M – внутренняя энергия одного моля вещества. Производная по темпе-

ратуре в (2.52) берется при условии постоянства объема, она является част-ной. Такие производные принято записывать в виде:

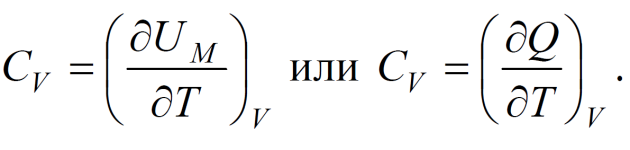
Внутренняя энергия определена с точностью до константы, т. к. в термоди-намике всегда рассматривается изменение этой величины в различных про-цессах. Поэтому из (2.52) или (2.53) следует:

U C T , 			m		.	(2.54)
	V	

Для изобарного процесса				первый закон термодинамики
QP  dU  pdV . Разделим это уравнение на dT, получим:
Q	P	C				V 
			P	C  p		 .
dT				V		T P

имеет вид

(2.55)

Воспользовавшись уравнением		состояния идеального газа,	найдем
VTP	 R p , тогда CP CV	R . После сокращения это уравнение
приобретает вид:
	CP  CV  R		(2.56)

Его называют уравнением Майера. Подставляя в (2.53) формулу (2.15), учи-тывая (2.56), получим:

C 	i	R ,	C	P		i  2	R .	(2.57)
V	2				2

Здесь i – число степеней свободы молекулы газа.

Ворпрос 45: Основные изопроцессы в идеальном газе

Изопроцессом называется термодинамический процесс, происходящий с газом при неизменном значении какого-либо его параметра. Рассмотрим изопроцессы в идеальном газе.

1. Изобарный процесс. Уравнение процесса можно получить из урав-нения Менделеева-Клапейрона при p  const .

V 	R	T  const T .	(2.58)
	p

На диаграмме V, T процесс имеет вид прямой, проходящей через начало ко-ординат. Работа в изобарном процессе:

V
A  2	pdV  pV2 V1 .	(2.59)
V1

2. Изохорный процесс. Аналогично получаем уравнение процесса при

V  const :

P 	R	T  const  T .	(2.60)
	V

На диаграмме p, T процесс имеет вид прямой, проходящей через начало ко-ординат. При неизменном объеме работа газа равна нулю.

3. Изотермический процесс. Уравнение процесса при Т  const имеет

вид:

pV RT  const .

(2.61)

На диаграмме p,V изотермический процесс изображается гиперболой p~ _V¹ .

Найдем работу газа в этом процессе:

V2	V2 dV			V2
A   pdV RT 			RT ln			.	(2.62)
		V			V
V	V			1
1	1

4. Адиабатический процесс. Такой процесс характеризуется отсутст-вием теплообмена с внешней средой. В течение процесса постоянной остает-ся энтропия S. Найдем уравнение процесса. Согласно первому закону термо-динамики при Q  0 :

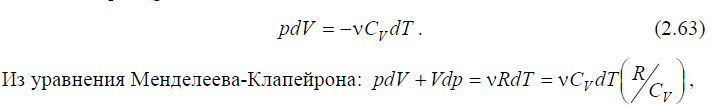
откуда выражаем C_V dT и подставляем в (2.63). С учетом (2.56), получаем:

C_P pdV  C_V Vdp  0

Разделяем переменные и интегрируем. Окончательно приходим к уравнению адиабатического процесса:

PV ^  const , (2.64)

где  ^CP _CV 1 – показатель адиабаты. Его можно представить через i –

число степеней свободы молекулы  ^{i }_i ²  1 ²_i . Работа в адиабатическом процессе равна:

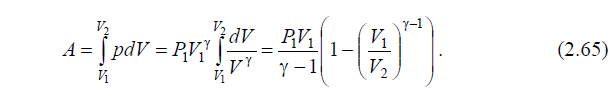
5. Политропический процесс. Этот процесс происходит с газом при постоянной теплоемкости C  const . Представим Q CdT , тогда первый

закон термодинамики примет вид CdT C_V dT  pdV или

C  CV dT  pdV  0 .							(2.66)
Из уравнения Менделеева-Клапейрона получаем:
	pdV  Vdp RdT .						(2.67)
Умножим (2.66) на	R	и	учтем		(2.67). Тогда		получаем:
C  CV pdV  Vdp pRdV  0 .		Раскрывая скобки, деля все					уравнение на
PV, получаем:
C  C	 R	pdV	 C  C		dp	 0 .	(2.68)
		V			p
V			V

Принимая во внимание уравнение Майера, интегрируем (2.68). Получаем в результате:

pV n  const ,

(2.69)

где n  ^{C  CP} – показатель политропы.

C  C_V

Работа в политропическом процессе имеет вид, подобный (2.65):

	PV			 V		n1
A 	1 1				1			.	(2.70)
	n 1			V2			
							

Следует заметить, что все рассмотренные в п. 1-4 процессы являются частным случаем политропического процесса. В каждом из них теплоемкость и n принимают частные значения, согласно таблице.

				Таблица 1
Процесс	Изобарный	Изохорный	Изотермический	Адиабатический
n	0	∞	1	γ
C	CP	CV	∞	0