Лекция № 3 Статистические игры

План лекции

1. Особенности принятия решений в условиях неопределённости. Построение матрицы игры и матрицы рисков.

2. Критерии принятия решений.

   1. Критерий Байеса.

   2. Критерий Лапласа

   3. Критерий Вальда.

   4. Критерий Сэвиджа.

   5. Критерий Гурвица.

1. Экономика и бизнес связаны с принятием решений в условиях неопределенности, т.е. отсутствия необходимой для обоснованного принятия решения информации.

Источники неопределённости:

• Нестабильность экономической и политической ситуации;

• Неопределённость действий партнёров по бизнесу;

• Недостаточная информация о спросе на товары и услуги

• Неизвестное качество сырья;

• Погодные и климатические условия и т.д.

Принятие управленческих решений предполагает наличие ситуаций выбора наиболее выгодного варианта поведения из нескольких имеющихся.

Такие задачи могут быть описаны матричными играми особого типа, в которых игрок взаимодействует с окружающей средой.

Отличительная особенность таких игр состоит в том, что в ней сознательно действует только один из участников. Объективно окружающая среда против игрока не действует. Она принимает одно из нескольких возможных состояний.

Методы принятия решений в играх с природой зависят от характера от того, известны или нет вероятности состояний окружающей среды, которую иногда называют «природа».

• Матричная игра, в которой игрок взаимодействует с окружающей средой, не заинтересованной в его проигрыше, и решает задачу определения наиболее выгодного варианта поведения с учётом неопределенности состояния окружающей среды, называется статистической игрой или игрой с природой.

• Сознательного игрока в таких играх называют ЛРП (лицо, принимающее решения).

Рассмотрим организацию и аналитическое представление игры с природой. Пусть сознательный игрок имеет m возможных стратегий: A₁, A₂, …, A_m.

У «природы» имеется n возможных состояний (стратегий): П₁, П₂, …, П_n.

Тогда условия «игры с природой» задаются матрицей A выигрышей игрока:

Таблица 1

	П1	П2	П3	….	Пn
A1	a11	a12	a13	…	a1n
A2	a21	a22	a23	…	a2n
…	…	…	…	…	…
Am	am1	am2	am3	…	amn

В некоторых случаях элементы этой матрицы могут рассматриваться как затраты (потери).

Другой способ задания матрицы игры с природой: в виде так называемой матрицы рисков

В данном случае величина риска — это размер платы за отсутствие информации о состоянии среды. Матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей A.

• Риском 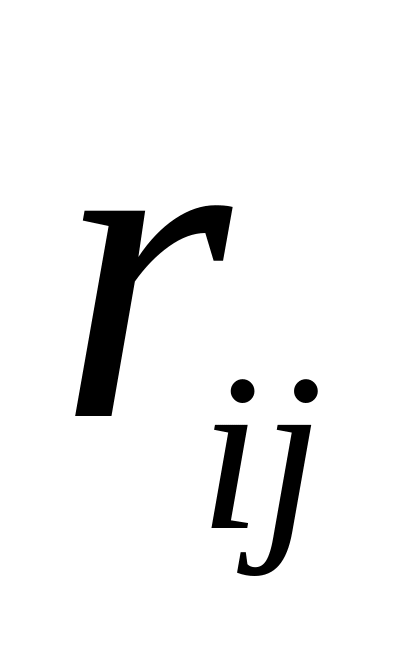игрока при использовании им стратегии и при состоянии «природы» называется разность между максимально возможным выигрышем при данном состоянии «природы» и выигрышем, который игрок получит реально, не имея этой информации.

(1)

Если элементы матрицы А — потери, то

(2)

Пример 1. Транспортное предприятие должно определить уровень своих производственных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги неизвестен, но прогнозируется, что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия. Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Возможные прогнозируемые затраты на развитие провозных возможностей представлены в табл. 2. Необходимо выбрать оптимальную стратегию развития предприятия.

 Таблица 2

Варианты  возможностей развития транспортного предприятия	Варианты спроса на транспортные услуги
	1	2	3	4
1	6	12	20	24
2	9	7	9	28
3	23	18	15	19
4	27	24	21	15