Раздел 3.Вопрос 9
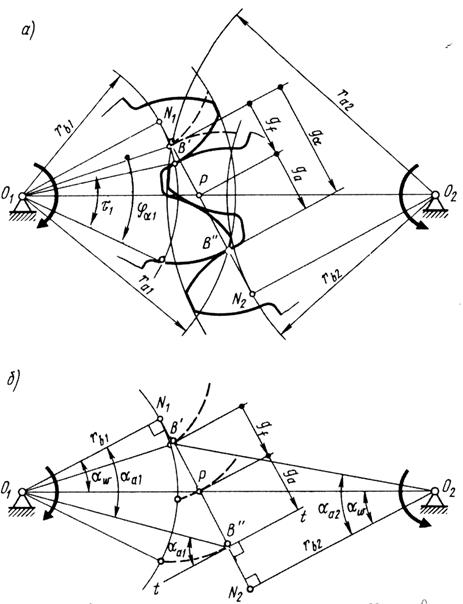
Качественные показатели зубчатой передачи.
Коэффициент перекрытия учитывает непрерывность и плавность зацепления в передаче. Такие качества передачи обеспечиваются перекрытием работы одной пары зубьев работой другой пары. Для этого каждая последующая пара зубьев должна войти в зацепление еще до того, как предшествующая пара выйдет из зацепления. О величине перекрытия судят по коэффициенту перекрытия, который выражают отношением угла торцового перекрытия к угловому шагу. Угол торцового перекрытия ja –– это угол поворота колеса от положения зубьев при входе в зацепление, когда они касаются в точке В', до положения зубьев при выходе из зацепления, когда они касаются в точке В"
Следовательно, коэффициент перекрытия прямозубой передачи
|
. (44)
Здесь 
––
угловой шаг; 
,
где 
––
длина активной линии зацепления. Она
складывается из длин дополюсной gf и
заполюсной ga частей активной линии
зацепления:
|
|
, (45)
. (46)
Подстановка
и в с учетом 
определяет
значение коэффициента перекрытия
прямозубой передачи
|
Если
при расчете по формуле (47) получится 
,
то в этом случае непрерывности процесса
зацепления зубьев не будет: одна пара
зубьев успеет выйти из зацепления еще
до того, как следующая пара зубьев войдет
в него. Поэтому минимально допустимым
значением ea является 1,05, которое
обеспечивает непрерывность процесса
зацепления с пятипроцентным запасом.
Важно отметить, что коэффициент перекрытия b уменьшается при увеличении коэффициентов смещения х1 и х2. Поэтому при проектировании передачи коэффициенты смещения надо назначать так, чтобы ea не получился бы меньше 1,05.
Продолжительность
зацепления одной пары зубьев в косозубой
передаче (
)
больше, чем в прямозубой (
).
Поэтому и коэффициент перекрытия
косозубой передачи egбольше ea и
подсчитывается по формуле
|
В
этой сумме слагаемое ea определяется
по формуле (47). Второе слагаемое 
.
Здесь 
––
ширина зубчатого колеса, y ––
коэффициент ширины зубчатого колеса,
назначаемый из условий прочности и
износостойкости зуба, 
––
осевой шаг косого зуба. Подставив b и рх
в выражение для eb, получим
|
Раздел 3 Вопрос 10
Зубчатая передача
механизм, состоящий из колёс с зубьями, которые сцепляются между собой и передают вращательное движение, обычно преобразуя угловые скорости и крутящие моменты.
З. п, разделяют по взаимному расположению осей на передачи: с параллельными осями — цилиндрические; с пересекающимися осями — конические, а также редко применяемые цилиндро-конические и плоско-цилиндрические; с перекрещивающимися осями — зубчато-винтовые (червячные, гипоидные и винтовые). Частным случаем З. п. является зубчато-реечная передача, преобразующая вращательное движение в поступательное или наоборот. В большинстве машин и механизмов применяют З. п. с внешним зацеплением, т. е. с зубчатыми колёсами, имеющими зубья на внешней поверхности, реже — с внутренним зацеплением, при котором на одном колесе зубья нарезаны на внутренней поверхности.
Зубчатые колёса выполняют: с прямыми зубьями для работ при невысоких и средних скоростях в открытых передачах и в коробках скоростей; с косыми зубьями для использования в ответственных передачах при средних и высоких скоростях (свыше 30% всех цилиндрических зубчатых колёс); с шевронными зубьями для передачи больших моментов и мощностей в тяжёлых машинах; с круговыми зубьями — во всех ответственных конических З. п. Как правило, в машинах и механизмах применяют З. п. с постоянным передаточным числом