3. Силовой анализ механизмов

1. Трение в кинематических парах. Влияние геометрических и физических

Характеристик элементов пары и смазочных материалов на величину трения и износа в паре.

2. Определение сил реакций в кинематических парах с учетом и без учета трения. Кинетостатика отдельных кинематических групп и всего механизма в целом. Явление самоторможения. Оценка качества механизма с помощью анализа углов давления.

3. Работа сил трения. КПД машин циклического действия. Определение КПД механизмов и их соединений. Понятие циркулирующего энергетического потока в замкнутых испытательных стендах и замкнутых механических передачах.

4. Виды неуравновешенности механизмов. Полное и частичное статические уравновешивания рычажных механизмов. Неуравновешенность роторов и методы их балансировки

Р3 В.1-1)Основная теорема зацепления (теорема Виллиса) Для постоянства передаточного отношения при зацеплении двух профилей зубьев необходимо, чтобы радиусы начальных окружностей зубчатых колёс, перекатывающихся друг по другу без скольжения, оставались неизменными. Если рассмотреть обращённое движение начальных окружностей, когда всей системе задана угловая скорость ( ), то второе колесо будет условно неподвижным и точка ^ Р является мгновенным центром относительного вращения колёс (рис. 70,а). Эта точка, называемая полюсом зацепления, где контактируют начальные окружности, делит межцентровое расстояние на отрезки, обратно пропорциональные угловым скоростям, т. к.

Рассмотрим обращённое движение профилей зубьев зубчатых колёс (рис. 70, б).

Точка контакта зубьев (точка к), принадлежащая первому колесу, вращается вокруг точки Р, которая будет мгновенным центром скоростей. Скорость   и совпадает с общей касательной к профилям в точке к при условии постоянства этого контакта. В  противном случае постоянного контакта не будет, так как появится составляющая   и профили разомкнутся (рис. 71). Так как рассматривается произвольное положение зубьев, то можно сформулировать теорему.  Нормаль NN к касающимся профилям зубьев,  рис. 71 проведённая через точку их касания, делит межцентровое расстояние на части, обратно пропорциональные угловым скоростям. Эта теорема, сформулированная Виллисом в 1841 г., определяет основной закон зацепления профилей, которые не могут быть произвольными, а должны быть специально подобраны.

Р3 В.2) Эвольвента и её свойства Наибольшее применение получили эвольвентные зубчатые передачи с профилем зубьев, очерченным по эвольвенте (рис. 72). ^ Эвольвентой круга называется траектория точки, лежащей на прямой, которая перекатывается без скольжения по окружности радиуса r_в, называемой основной. Эвольвента имеет следующие свойства: 1) начинается с основной окружности; 2) нормаль к эвольвенте является касательной к основной окружности; 3) радиус кривизны эвольвенты в каждой её точке лежит на нормали к эвольвенте в этой точке. Основная окружность представляет собой геометрическое место центров кривизны эвольвенты и является её эволютой.

Р3 В.3) Основные параметры зубчатых колёс Основными параметрами зубчатого колеса являются (рис. 75): z – число зубьев; r_a – радиус (диаметр) окружности  выступов; r_f – радиус (диаметр) окружности  впадин; r_b - радиус (диаметр) основной окружности; r - радиус (диаметр) делительной  рис. 75 окружности, т. е. окружности, ко- торая является начальной в станочном зацеплении колеса с режущим инструментом; р – шаг по делительной окружности; h – высота зуба, равная h=h_a+h_f, где: h_a – высота головки зуба; h_f – высота ножки зуба; m – модуль зацепления, определяемый из условия: , т. е.   (измеряется в мм). Величина m стандартизирована, а делительная окружность является окружностью стандартного модуля. Обычно размеры зубчатого колеса и зубьев выражаются через m.  ^ Так, например:  , где   - коэффициент высоты головки зуба; , где   - коэффициент радиального зазора; ;  ;  , где α – угол исходного контура режущего инструмента. Обычно для стандартных зубчатых колёс:  ;  ; α=20º.

 

Р3 В.4) Методы нарезания зубчатых колёс Существует два принципиально различных метода нарезания: 1) метод копирования; 2) метод обкатки. В первом случае впадина зубчатого колеса фрезеруется на универсальном фрезерном станке фасонными дисковыми или пальцевыми фрезами, профиль которых соответствует профилю впадины (рис. 76). Затем заготовку поворачивают  на угол 360º/Z и нарезают следующую впадину. При этом используется делительная головка, а также имеются наборы фрез для нарезания колёс с различным модулем и различным числом зубьев. Метод непроизводителен и применяется в мелкосерийном и единичном производстве. рис. 76 Второй метод обката или огибания может производиться с помощью инструментальной рейки (гребёнки) на зубострогальном станке; долбяком на зубодолбёжном станке или червячной фрезой на зубофрезерном станке. Этот метод высокопроизводителен и применяется в массовом и крупносерийном производстве. Одним и тем же инструментом можно нарезать колёса с различным числом зубьев. Нарезание с помощью инструментальной рейки имитирует реечное зацепление (рис. 77, а), где профиль зуба образуется как огибающая последовательных положений профиля инструмента, угол исходного контура которого α=20º (рис. 77, б). Зацепление между режущим инструментом и нарезаемым колесом называется станочным. В станочном зацеплении начальная окружность всегда совпадает с делительной. Самым производительным из рассмотренных методов является зубофрезерование с помощью червячных фрез, которые находятся в зацеплении с заготовкой по аналогии с червячной передачей (рис. 77, в). При нарезании долбяком осуществляется его возвратно поступательное движение при одновременном вращении. Фактически при этом осуществляется зацепление заготовки с инструментальным зубчатым колесом – долбяком (рис. 77, г). Этот метод чаще всего используется при нарезании внутренних зубчатых венцов. 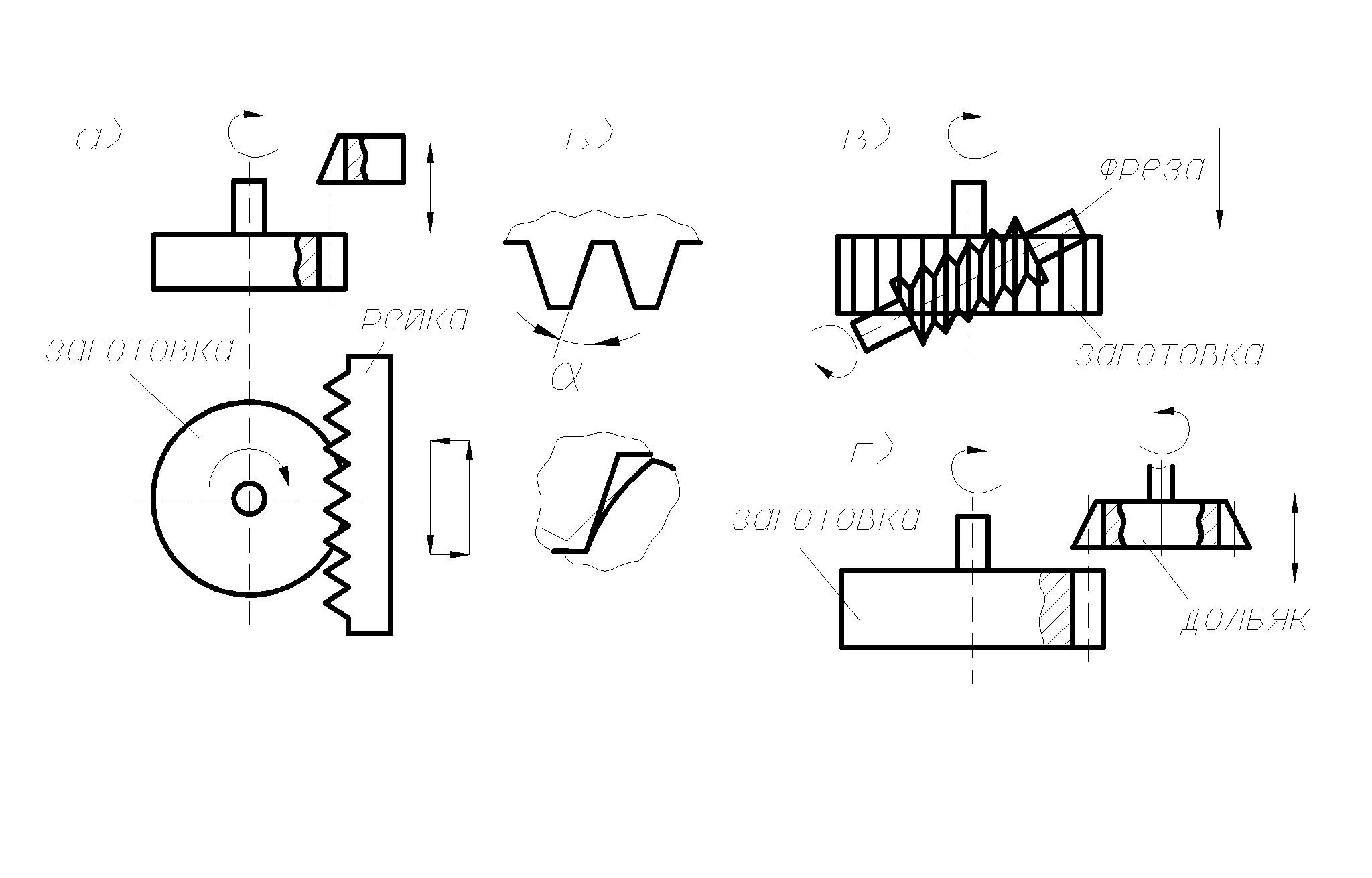рис. 77 Все рассмотренные методы используются для нарезания цилиндрических колёс как с прямыми, так и с косыми зубьями.