Р.1В.1
Машины: – это система, созданная трудом человека для изучения и использования законов природы с целью облегчения физического и умственного труда, увеличения его производительности и облегчения путем частичной или полной замены человека в его трудовых и физиологических функциях.
Машина есть устройство, выполняющее механические движения для преобразования энергии, материалов и информации.
Механизм – это система тел, предназначенная для преобразования движения одного или нескольких тел в требуемое движение других тел.
В зависимости от назначения (от вида преобразования) различают энергетические, техно-логические, транспортные и информационные машины.
Энергетические машины предназначены для преобразования любого вида энергии в механическую энергию (и наоборот). Электродвигатели, двигатели внутреннего сгорания, турбины и т.п. – примеры энергетических машин.
Технологические машины предназначены для изменения формы, размеров, свойств или состояния исходных материалов и заготовок. К ним относятся металлообрабатывающие станки и комплексы, кузнечно-прессовое оборудование, прокатные станы, литейное оборудование, полиграфические, пищевые и другие машины.
Транспортные машины предназначены для перемещения людей, грузов, инструментов и других объектов в пространстве с требуемой скоростью.
Информационные машины предназначены преобразовывать вводимую информацию для контроля, регулирования и управления движением.
Механизмы разделяют: на элементарные, простые, с постоянной структурой, с переменной структурой, с незамкнутыми кинематическими цепями, с замкнутыми кинематическими цепями, стационарные, нестационарные, сложные, однотипные, многотипные, комбинированные.
Элементарный механизм- механизм, который нельзя более расчленить на части, способные самостоятельно преобразовывать движение.
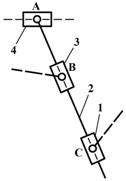
Элементарный механизм (рис.1.3) представляет собой подвижное звено 1 и стойку 0, объединенные между собой посредством кинематической пары. На рис.1.3, а представлена схема элементарного вращательного механизма, на рис.1.3, би в – соответственно цилиндрического и сферического элементарных механизмов. Кинематические пары обозначены: А –вращательная, В – цилиндрическая иС – сферическая.
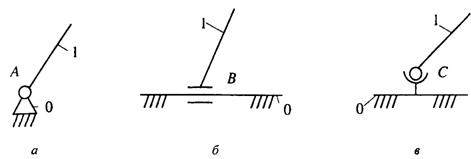
Рис. 1.3. Схемы элементарных механизмов
Простой механизм– механизм, состоящий из элементарного(ных) механизма(ов) с присоединенной к нему (ним) одной структурной группой (ступенью).
Простыми механизмами являются шарнирный четырех- и пятизвенник, кулисный, кулачковый, зубчатый, мальтийский и т. п.
Механизм с постоянной структурой – механизм, кинематическая цепь которого в процессе функционирования структурно не изменяется.
Механизм с переменной структурой– механизм, кинематическая цепь которого в процессе функционирования структурно изменяется.
Механизм с незамкнутой кинематической цепью– механизм, который имеет в своем составе только незамкнутые кинематические цепи.
Механизм с замкнутой кинематической цепью– механизм, который имеет в своем составе только замкнутые кинематические цепи.
Стационарный механизм– простой механизм, присоединенный своими внешними кинематическими парами только к неподвижной стойке.
Нестационарный механизм– простой механизм, закрепленный своими внешними кинематическими парами на подвижных звеньях другого механизма.
Простые подвижные механизмы могут иметь как замкнутую, так и незамкнутую кинематическую цепь.
Сложный механизм– механизм, состоящий из элементарного(ых) механизма(ов), к которому(ым) присоединены две или более структурные группы (ступени), простой(ые) механизм(ы).
Сложный однотипный механизм– механизм, в состав которого входят только элементарные механизмы, структурные группы и простые механизмы, имеющие одинаковые количественные и видовые простейшие перемещения звеньев и элементов кинематических пар.
Многотипный сложный механизм– механизм, в состав которого входят элементарные механизмы, структурные группы и простые механизмы, существующие в различных пространствах (поверхностях).
Комбинированный механизм– механизм, образованный в результате произвольного объединения как простых, так и сложных механизмов с замкнутыми и незамкнутыми кинематическими цепями.
Цель ТММ - анализ и синтез типовых механизмов и их систем. Задачи ТММ: разработка общих методов исследования структуры, геометрии, кинематики и динамики типовых механизмов и их систем.
Р.1В2
Механизмы состоят из звеньев и кинематических пар.
Звено- одно или несколько жестко соединенных твердых тел.
Кинематическая пара- соединение двух звеньев, допускающее относительное движение.
Система звеньев соединённых между собой кинематическими парами называется кинематической цепью
Основные виды звеньев: стойка, кривошип, коромысло, ползун, кулиса, кулачок, зубчатое колесо.
Р.1В.3
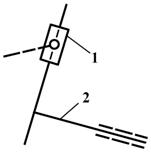
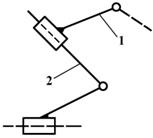
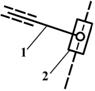
Классификация кинематических пар
В пространстве любое тело имеет 6 степеней свободы (W), т.е. может совершать 6 независимых движений: 3 поступательных вдоль выбранных осей и 3 вращательных вокруг этих же осей. Величины соответствующих перемещений называют обобщенными координатами. Если такое тело связать с другим телом посредством кинематической пары, то это уменьшит его число степеней свободы на число наложенных связей (S), налагаемых другим телом. Число связей определяется видом кинематической пары. Значит, справедлива запись:
W+S=6
Классификация кинематических пар проводится по числу наложенных связей:
S=1, W=5 — кинематическая пара 1 класса
S=2, W=4 — кинематическая пара 2 класса
S=3, W=3 — кинематическая пара 3 класса
S=4, W=2 — кинематическая пара 4 класса
S=5, W=1 — кинематическая пара 5 класса
Р.1В.4
Структурный анализ механизма
При анализе структурной схемы механизма определяют число подвижных звеньев, вид кинематических пар, число степеней свободы механизма, число замкнутых контуров и их класс, число избыточных контурных связей.
Число W степеней свободы пространственного механизма равно разности между общим числом координат подвижных звеньев и числом уравнений, связывающих эти координаты
Для плоских механизмов пары могут быть одноподвижными (низшие) и двухподвижными (высшие), и они не связаны с видами пар, различаемых по подвижности, так как звенья совершают только плоское движение. Тогда число WП степеней свободы плоского механизма определяется выражением
WП = 3n – 2p1 – p2 = 3n – 2pн – pв,(2.2)
где pн, pв – число низших и высших пар соответственно. Это соотношение опубликовано П.Л. Чебышевым в 1869 г. в несколько иной форме. Однако выражение (2.2) в литературе называют формулой Чебышева.
Р.1В.5
Структурный анализ механизма
При анализе структурной схемы механизма определяют число подвижных звеньев, вид кинематических пар, число степеней свободы механизма, число замкнутых контуров и их класс, число избыточных контурных связей.
Гру́ппа Ассу́ра это образованная только подвижными звеньями механизма кинематическая цепь, подвижность которой равна нулю[1].
Группы Ассура делятся по классификации И.И. Артоболевского на классы, порядки и виды. Класс группы задается наивысшим замкнутым контуром, входящим в ее состав. Класс же контура определяется числом внутренних кинематических пар, образующих этот замкнутый контур. Можно сказать, что:
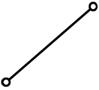
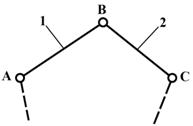
а) в группу Ассура II-го класса входит прямолинейный контур (табл.3);
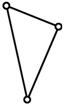
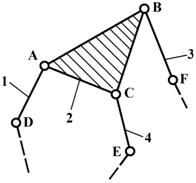
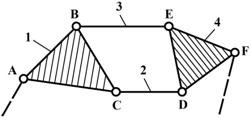
б) в группу Ассура III-го класса – трехсторонний контур ABC (рис.4,б);
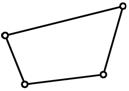
в) в группу Ассура IV-го класса – четырехсторонний подвижный контур BCDE.
Таблица 3
Классы контуров |
||||
II |
III |
III |
IV |
V |
|
|
|
|
|
Модификации групп Ассура II, III, IV классов представлены на рис.4.
а) |
б) |
в) |
||
г) |
д) |
|||
|
|
|
|
|
Рис.4. Группы Ассура: а) II-го класса; б) в) г)III-го класса; д) IV-го класса
Группы Ассура II класса содержат два звена и три кинематических пары. Разновидности групп Ассура II класса изображены на рис.5:
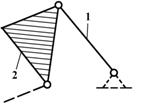
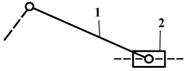
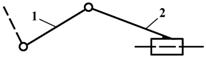
вид 1 – все кинематические пары вращательные;
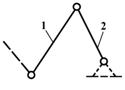
вид 2 – одна крайняя кинематическая пара – поступательная, а все остальные – вращательные;
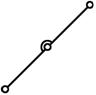
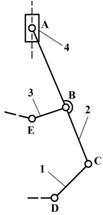
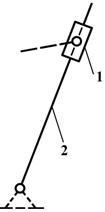
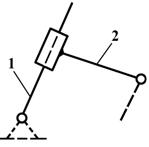
вид 3 – звенья соединены между собой поступательной кинематической парой, а крайние пары являются вращательными;
вид 4 – звенья соединены вращательной парой, а обе крайние кинематические пары – поступательные;
вид 5 – одна крайняя кинематическая пара – вращательная; все остальные – поступательные.
Вид 1
|
Вид 2
|
Вид3
|
|
Вид 5
|
|
||
Вид 4
|
|
Рис. 5. Группы Ассура II -го класса различных видов.
Порядок группы Ассура определяется количеством кинематических пар, которыми она присоединяется к другим звеньям, т.е. числом ее внешних (свободных) пар.
В группе Ассура на Рис.4-б звено 2, называемое базисным, входит в три внутренние кинематические пары со звеньями 1,3 и 4. Звенья 1,3,4 называются поводками и своими внешними кинематическими парами присоединяются к другим звеньям механизма. Эта группа называется трехповодковой, или группой Ассура III класса III порядка.
Р.1В.6
Решение задачи начинается с определения числа степеней свободы кинематической цепи, положенной в основу данного механизма. В соответствии с числом степеней свободы назначается число начальных звеньев (или входных звеньев), после чего цепь становится механизмом. После присоединения каждой группы Ассура должен получаться промежуточный механизм, с тем же числом степеней свободы, что и заданный. После присоединения последней группы должен получиться первоначально заданный механизм.
Класс механизма определяется наивысшим классом структурной группы, входящей в механизм.
Порядок группы определяется числом кинематических пар, которыми группа присоединяется к основному механизму. Пунктирными линиями показаны звенья, к которым звенья присоединяется. Этими звеньями могут быть стойка или другие звенья.
Группа, имеющая два звена и три кинематические пары 5-го класса (n = 2, p5 = 3), называется группой II класса 2-го порядка или двухповодковой группой .
Группы второго класса и второго порядка (n = 2, p5 = 3), делятся на 5 видов, которые определяются взаимным расположением вращательных и поступательных пар.
В группе 1-го вида – все пары вращательные;
в группе 2-го вида – на конце одного из звеньев поступательная пара;
в группе 3-го вида – в середине поступательная пара;
в группе 4-го вида – на конце обоих звеньев поступательные пары;
в группе 5-го вида – в середине и на конце одного из звеньев поступательные пары.
Р.1В.7
Для любого плоского механизма, содержащего высшие кинематические пары, можно построить так называемыйзаменяющий механизм, который не содержит высших пар, но эквивалентен заменяемому механизму по следующим показателям:
1) в структурном отношении (имеет ту же подвижность);
2) в отношении кинематики (при тех же законах движения входных звеньев остаются прежними законы движения выходных, сохраняются также траектории и законы движения всех точек);
3) в силовом отношении.
Если высшая пара образована профилями переменной кривизны, то вместо термина «заменяющий» используют «мгновенно-заменяющий».
При выполнении процедуры замены каждой высшей пары вводится так называемое фиктивное звено (на рис. 2.19 обозначено буквой Ф), участвующее в двух парах пятого класса: либо в поступательной и вращательной (если один из профилей – прямая), либо в двух вращательных парах.
Центры шарниров фиктивных звеньев всегда совпадают с центрами кривизны контактирующих профилей.
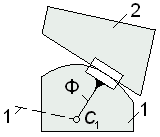
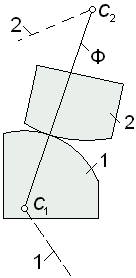
а) б)
Рис.2.19. Принцип построения заменяющих схем