Расчет реактора типа ввэр

Активная зона реактора собрана из стержней, объединенных в шестигранные кассеты (рис, 11). Стержни омываются снаружи обычной водой под давлением. Выпишем нужные для расчета ис­ходные данные.

1. Замедлитель - вода при средней температуре и Давлении p=100 ата. При этих параметрах

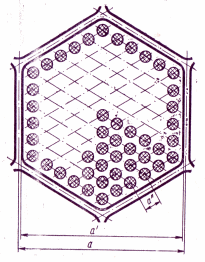
Рис. 11. Поперечный разрез кассеты реак­тора ВВЭР.

Замедлитель служит одновременно и теплоносителем, причем

2. Тепловыделяющие элементы — стержневые с наружным ох­лаждением. Размеры (см. рис. 9б): (толщина покрытия элементов ).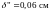

В каждой кассете содержится n = 91 элемент. В кассете эле­менты образуют треугольную решетку с шагом Раз­мер кассет «под ключ» 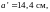толщина оболочки кассеты 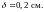Шаг установки кассет т. е. между кассетами имеется щель размером Материал оболочек твэлов и кассет — цирконий с добавкой 1% ниобия.

3. Ядерное горючее - 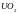с плотностью Обо­гащение урана в

4. Общие характеристики реактора. Мощность N=750 Мвт. Средний тепловой поток на поверхности твэлов

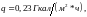
отражатель водяной; реактор цилиндрический с соотношением размеров

H = 0,85 D,

т.е. m = 0,85. Все эти характеристики взяты из работы [3] (стр. 105).

Тепловой расчет

Задано 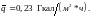Находим среднюю энергетическую нагрузку объема активной зоны:

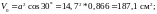
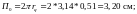
Оцениваем размеры активной зоны, приняв

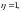
Отсюда

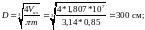
Вычисляем скорость теплоносителя в пространстве между теп­ловыделяющими элементами. Площадь теплоносителя в кассете, приходящаяся на один твэл, равна

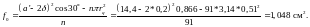
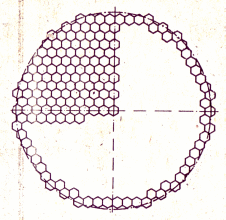
Рис. 12. Схема поперечного разреза активной зоны реактора ВВЭР.

При следовательно,

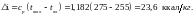
Зададимся радиальным коэффициентом неравномерности и тогда максимальная скорость воды в среднем сечении реактора

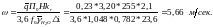
Выбираем форму сечения активной зоны, изображенную на рис. 12;

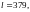следовательно,

Высоту H принимаем равной 255 см.

Физический расчет

Вычисляем объемы веществ 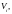приходящиеся на 1 см длины кассеты.

Объем горючего (двуокиси урана)

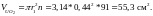
Объем оболочек твэлов

Объем оболочки кассеты

Общий объем циркониевого сплава

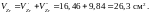
Объем воды в кассете

Объем воды в зазоре между кассетами

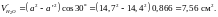
Общий объем воды

Определяем ядерные концентрации веществ: при

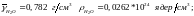
при

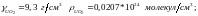
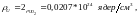
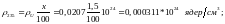
Удельный вес цирконий - ниобиевого сплава принимаем рав­ным удельному весу циркония (см., например работу [6], стр. 249). Можно считать, что

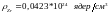
Плотность ниобия подсчитаем по формуле

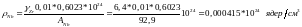
Полученные результаты сведем в табл. 10.

ТАБЛИЦА №10

Вещество
	55,3	0,00031	694	10	-	-		11,94		-
	55,3	0,0204	2,7	8,3	-	-		3,04		-
	55,3	0,0414	<0,0002	3,8	0,120	0,456		~0		1,05
	26,3	0,0423	0,191*	6,2	0,0218	0,135		0,21		0,15
	103,0	0,0262	0,66	-	-	42,5		1,78		114,7
							16,97		115,9
* С учетом добавки 1% Nb

В этой таблице добавка ниобия к цирконию учтена тем, что сечение поглощения циркония принято равным

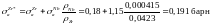
На все же другие характеристики присутствие ниобия влияет очень мало.

Теперь вычислим макроскопические сечения, нужные для расче­та температуры нейтронного газа. Пользуясь табл. 10, находим

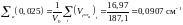
Средняя температура замедлителя

Находим температуру нейтронного газа

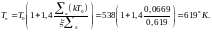
Для удобства пользования таблицами принимаем

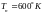
Задавшись 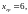находим в справочнике [6] при сечение урана -235, усредненное но спектру Максвелла,

Чтобы получить усредненные сечения других элементов, умножаем величины на

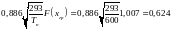
Вычисляем 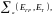используя данные табл. 10:

из рис. 3 находим 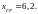Будем считать, что совпадение с первоначально заданным значением удовлетворительное. Таким обра­зом, получаем сечения, принимая

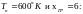
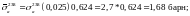
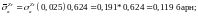
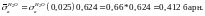
По формулам (25) и (28) находим также транспортные сече­ния для тепловых нейтронов и все результаты сводим в табл. 11. Сечения (1 эв) для краткости будем обозначать

ТАБЛИЦА №11

Вещество
	55,3	0,00031	403	413	9,97	6,93	7,1	0,2
	55,3	0,0204	1,68	9,96	8,28	1,89	11,3	9,3
	55,3	0,0414	~0	3,64	3,64	~0	8,3	8,3
	26,3	0,0423	0,119*	6,28	6,16	0,13	7,0	6,9
	103,0	0,0262	0,412	48,2	17,5	1,11	130,1	47,2
						10,06	163,8	71,9
* С учетом добавки 1% Nb/

Ввиду того, что диаметр тепловыделяющих элементов мал и они образуют в кассете тесную решетку, микроскопическая нерав­номерность нейтронного потока в тепловой группе нейтронов до­лжна быть довольно слабой, поэтому будем рассчитывать все усредненные характеристики активной зоны (кроме ( - вероятно­сти избежать резонансный захват) методом простой гомогенизации).

По формулам типа (18) находим для активной зоны:

Сравнивая величину с шагом решетки видим, что они примерно одинаковы. Следовательно, Мик­роскопическая неравномерность потока в ячейках решетки в самом деле не может быть очень большой.

Вычислим теперь групповые коэффициенты диффузии и квадрат длины диффузии тепловых нейтронов

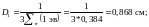
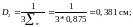
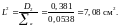
Квадрат длины замедления найдем с помощью рис. 5. Запи­шем объемы урана и воды, приведенные к плотности при нормаль­ных условиях;

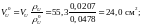
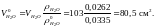
Присутствие циркония и кислорода (в составе ) учтем при­ближенно, заменив их некоторым «эквивалентным» объемом урана 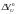с учетом разницы в плотностях и сечениях рассеяния. Определим

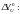
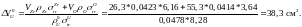
Надо сказать, что такая замена в действительности не эквивалентна. Она не учитывает, например, различия в замедляющих свойствах, которые у тяжелых металлов определяются в большой степени сечением неупругого рассеяния. Более Точные результаты можно было бы получить по формуле (76) или при непосредствен­ном измерении в среде заданного состава. Описанный выше прием использован только для упрощения вычислений в рассматриваемом примере.

Значение функции 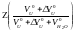находим из рис. 5,

вычислив предварительно аргумент:

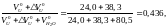
Тогда Следовательно,

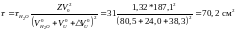
Учитывая, что эта величина вычислена, вероятно, с большой по­грешностью, примем

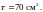
Перейдем к расчету Коэффициент вычислим по формуле (46) при f = 1 используя данные

табл. 11:

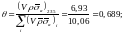
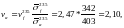
По формуле (56) вычисляем

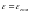
(здесь совсем не учитываются цирконий и кислород, так как их замедляющая способность мала по сравнению с водой, и они не обладают способностью к делению).

Коэффициент вычисляем по формуле (72), принимая (из-за отсутствия расчета теплопередачи в тепловыделяющих элементах) среднюю температуру урана Найдем сначала

Подставив их в формулу (72), получим

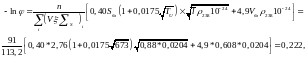
Тогда

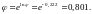
В результате

Оценим теперь величину k. Вместо отражателей прибавим к размерам активной зоны эквивалентные добавки 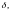одинаковые со всех сторон и равные 12 см (характерные для водяных отражателей). Тогда

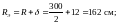
следовательно,

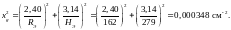
По формуле (81) получаем

Поскольку в рассматриваемом случае эквивалентная добавка мала по сравнению с R и H, то погрешность в ее определении не очень существенна для k. Для простоты вычислим эквивалентную добавку (с вполне удовлетворительной точностью) по формулам сферической геометрии (93), (95). Примем температуру воды в отражателе 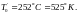При этом плотность воды 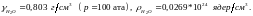В отражателе отношение мало, поэтому можно считать, что Тогда

Для надтепловых нейтронов

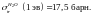
Вычисляем макроскопические характеристики отражателя:

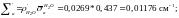
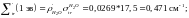
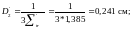
Толщину отражателя h будем считать практически бесконечной. Используя приближенную величину 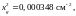находим радиус 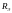сферического реактора

Отсюда

Далее по формулам (88) — (94) получаем:

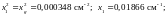
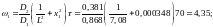
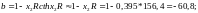
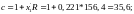
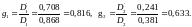
После подстановки всех этих величин в формулу (92) получаем

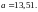
Из уравнения (96) определяем 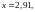откуда

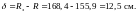
Как видим, ранее принятое значение мало отличается от вычисленного, и поэтому величина получилась практически точной.

Расчет изменения изотопного состава во времени, определение кампании реактора и расчет системы регулирования ведут точней так же, как в предыдущем примере.

121