16) Понятие о ядре сечения при внецентренном растяжении или сжатии и порядок его построения.

В большинстве случаев строительные конструкции изготавливаютсяиз хрупких материалов (кирпич, бетон, железобетон). Эти материалы хорошо работают на сжатие, но имеют низкую прочность при растяжении, поэтомупри их использовании необходимо определить положение ядра сечения.

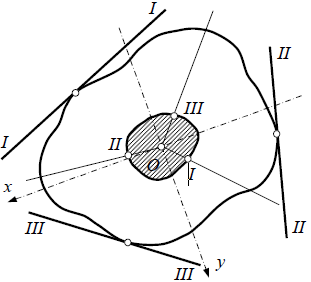
Рассмотрим случай внецентренного сжатия стойки произвольного поперечного сечения. Предположим, что точка приложения внецентренной силы F перемещается по прямым, проходящим через центр тяжестиСпоперечного сечения стойки. Каждая изнейтральных линий будет перемещатьсяпараллельно самой себе. При приложении сжимающей силы F в некоторых

граничных точкахI, II и III, принадлежащих ранее указанным прямым, нейтральные линии I-I, II-II и III-IIIстановятся касательными к внешнемуконтуру поперечного сечения. Таккак эти нейтральные линии не пересекают сечениестойки, то все ее продольные волокна будут работатьтолько на сжатие.

Если через центр тяжести сеченияОпровестибесчисленное множество прямых, то для каждойиз них можно установитьтакое положение граничных точек, когда нейтральная линия становится касательной квнешнему контуру поперечногосечения. Совокупность этих точекобразует границу некоторой замкнутойобласти, называемой ядром сечения. Любая продольнаясила, приложеннаявнутри ядра сечения, будетвызывать только сжимающие или растягивающие нормальные напряжения. Из уравненийполучаем следующиевыражения длявычисления координат точек, принадлежащихгранице ядрасечения

Таким образом, ядром сечения называетсязамкнутая выпуклая область, очерченная вблизи центра тяжести поперечного сечения, характеризующаяся тем, что внецентреннаясосредоточенная сила, приложеннаявнутри этой области, создает во всех волокнах стойкиодин вид простойдеформации – растяжение илисжатие.

Чтобы построить ядро сечения, необходимопровести все возможныекасательные к внешнему контуру поперечного сечениявнецентренно нагруженной стойки, предполагая, чтоэти касательные являются нейтральными линиями. Для каждой касательной можноопределить отрезки х a иу a , отсекаемые ими отглавных центральных осей поперечного сечениястойки и определяемые в соответствии свыражениямикоординатыграничных точек ядра сечения. Соединяя полученные точки, получаем искомое ядро сечения.

17)Определение нормальных напряжений при косом изгибе

Используя принцип независимости действия сил (принцип суперпозиции) найдем напряжения при косом изгибе. Рассмотрим точку A с координатами (y, z) в сечении изгибаемой балки и определим в ней напряжения от каждого из внутренних усилий, возникающих при косом изгибе:

-нормальные напряжения от изгибающего момента Mz