13)Определение нормальных напряжений при внецентренном растяжении или сжатии короткой стойки.

Внецентренное растяжение или сжатие является частным случаем

сложного сопротивления прямого бруса. Загружение стержня осуществляется сосредоточенной силой, действующей параллельной его оси Оz, приэтом точка ее приложения не совпадает с центром тяжести поперечногосечения С.Внецентренное растяжение (сжатие) испытывают короткие стержни.Все сечения являются равноопасными, поэтому нет необходимости в построении эпюр внутренних силовых факторов. При загружении стержнявнецентренной силой в егопроизвольном поперечном сечении возникают три внутренних силовых фактора: продольная сила Nzи два изгибающихмомента Mxи My. Величины внутренних усилий могут быть определены изуравнений статического равновесия:

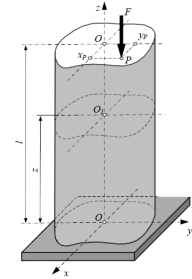
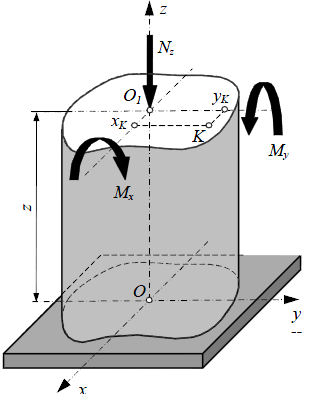
Рассмотрим поперечное сечение стержня на расстоянии z от началакоординат. Вычислим нормальные напряжения в некоторой точке K, принадлежащей этому сечению. Точка K в системе главных центральных осей имеет положительные координаты хKи уK. Придействии заданной силы продольное волокно стержня, которому принадлежит точка

K, будет испытывать сжатие, как от продольной силы z N , так иот изгибающих моментов Mxи My. Воспользовавшись принципомнезависимости действия сил, получаем

Полученная формула позволяет вычислять нормальные напряженияв любой точке внецентренно сжатого стержня. Следует заметить, что знакв уравнении зависит от заданного направления внешней внецентренно действующей силы.

14) Определение положения нейтральной линии при внецентренном растяжении или сжатии

При внецентренном растяжении или сжатии короткойстойки в ее поперечном сечении

появляется нейтральная линия, разделяющая области растяженияи сжатия продольных волокон. Таким образом, привнецентренном растяжении илисжатии поперечное сечение поворачивается вокруг нейтральнойлинии.

Условием существованиянейтральной линии является равенство нулю выражения

Обозначим координаты любойточки, принадлежащей нейтральной линии, как хNи уN. Тогда положениенейтральной линии может быть определено из следующего уравнения:

Обозначим отрезки, отсекаемые нейтральной линией от главных осей поперечного сечения стержня, как х а и у а.Тогда из уравненияполучаем

Полученные отрезки х a и у a в выбранном масштабе показываем начертеже. В результате на главных осях поперечного сечения имеем две

точки E и D соответственно. Соединяя эти точки прямой N-N, получаемискомое положение нейтральной линии.

15) Основные свойства нейтральной линии при внецентренном растяжении или сжатии.

При изгибе бруса часть волокон между двумя взятыми произвольно поперечными сечениями удлиняются, часть — укорачиваются. В случае простого (плоского) изгиба в месте перехода от вытянутых волокон к сжатым расположен бесконечно тонкий слой, перпендикулярный плоскости изгиба (плоскости изогнутой оси бруса), в которой расстояние между поперечными плоскостями, а, следовательно, и длина волокон не изменяются. Пересечение этого нейтрального слоя с поперечным сечением дает нейтральную ось последнего. Если все внешние силы, действующие на прямой брус (включая реакции опор), расположены в плоскости изгиба перпендикулярно к изогнутой оси бруса, то нейтральный слой совпадает с осевым слоем, а нейтральная ось образуется пересечением этого слоя с поперечным сечением. Если нейтральный слой между двумя поперечными сечениями расположен вне бруса, то все волокна бруса между этими сечениями либо растянуты, либо сжаты (один из случаев в сложном изгибе). Нейтральную ось также называют нулевой осью (нулевой линией), так как в ней удлинение волокон, а следовательно и продольное напряжение, равно нулю.