23. Точность оценки, доверительная вероятность (надежность).

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, - точечные.

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами -концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.

Пусть найденная по данным выборки статистическая характеристика Θ*служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом (Θ может быть и случайной величиной). Ясно, что Θ* тем точнее определяет параметр Θ, чем меньше абсолютная величина разности |Θ - Θ*|.

Другими словами, если δ>0 и |Θ - Θ*|<δ, то чем меньше δ, тем оценка точнее.

Таким образом, положительное число δ характеризует точность оценки. Однако статистические методы не позволяют категорически утверждать,что оценка Θ* удовлетворяет неравенству |Θ - Θ*|<δ; можно лишь говорить о

вероятности γ, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность γ, с которой осуществляется неравенство |Θ - Θ*|<δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число,близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0.999.

Пусть вероятность того, что |Θ - Θ*|<δ, равна γ

Заменив неравенство |Θ - Θ*|<δ равносильным ему двойным неравенством

–δ<Θ - Θ*<δ, или Θ*–δ<Θ< Θ*+δ, имеем

Это соотношение следует понимать так: вероятность того, что интервал(Θ*–δ, Θ*+δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.

24. Доверительный интервал.

Доверительным называют интервал (Θ*–δ, Θ*+δ), который покрывает неизвестный параметр с заданной надежностью γ.

25. Определение вероятности

Вероятность – число, характеризующее степень возможности появления события. Каждый из возможных результатов испытания – элементарный исход. Элементарные исходы, где интересующее нас событие наступает – благоприятствующий исход этого события. Отношение числа благоприятных событию А элементарных исходов к их общему числу называется вероятностью события А, и обозначается Р(А).

Р(А) = m / n

26. Вероятность появления хотя бы одного события.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий P(A)+P(B) без вероятности их совместного события

P(A+B)=P(A)+P(B)=P(AB)

Вероятность попадания в цель из орудия A = 0,7, из орудия B = 0,8

Найти вероятность попадания при залпе хотя бы одним орудием

0,7*0,8=0,56

0,7+0,8-0,56-0,94

27. Формула полной вероятности

Пусть событие A может наступить при условии появления одного из совместных событий P(A), P(B) … P(n), которые образуют полную группу

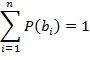
b₁, … , b_i, … ,b_n

Пусть известны вероятности этих событий и все условные вероятности b₁, b₂, … , b_n

Найти вероятность события A.

Вероятность события A, которое может наступить только лишь с появлением одного из событий b равна сумма произведения b_i на условную вероятность.

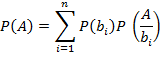
Имеются 2 набора деталей. Вероятность того, что деталь первого набора стандартная 0,8, из второго 0,9.

Вероятность того, что случайно взятая деталь стандартная равна:

Выбранная деталь стандартная = A

P(B₁)=0,5 P(B₂)=0,5

P(A)=P(B₁)*P(A/B₁)+P(B₂)*P(A/B₂)=0,4+0,45=0,85