1.5. Специальная теория относительности

Специальная теория относительности (С.Т.О.) изучает свойства пространства и времени как двух форм существования материи в инерциальных системах отсчета. Обычно для удобства выбирают две ИСО – неподвижную С.О. К с осями координат Ох, Оy, Оz и движущуюся относительно нее с постоянной скоростью вдоль совпадающих осей Ох и О^’х^' систему отсчета К´ (оси Оу и О^'у^', Оz и О^'z^' при движении остаются параллельными). В начальный момент времени (t=0) начала координат этих систем отсчета – точки О^' и О^' совпадают (рис.1.29).

Отметим общие свойства пространства и времени, подтвержденные опытными фактами и не зависящие от рассматриваемых теоретических моделей: пространство является однородным и изотропным, а время является однородным.

Рис. 1.29

1.5.1. Преобразования Галилея. Принцип относительности Галилея

В классической механике считается, что предельная скорость передачи взаимодействий в природе может быть бесконечно большой ( ), что приводит к дополнительным свойствам пространства и времени. К ним относятся следующие свойства пространства и времени: пространство и время абсолютны, не связаны друг с другом; время течет одинаково во всех ИСО (t=t'); пространство и время не зависят от наличия вещества, пространство является пустым вместилищем материальных тел.

Дополнительные свойства пространства и времени, возникающие в классической механике, позволяют получить преобразования Галилея – это формулы, связывающие координаты и время одного и того же события в разных ИСО. Под событием понимают любое явление (выстрел из ружья, рождение частицы и т.д.), происходящее в одной точке пространства в какой-либо момент времени.

Пусть в точке М (рис.1.29) происходит какое-либо событие, координаты и время которого в С.О. К – (x, y, z, t), а в С.О. K' – (x', y', z', t'). Учитывая расположение точки М (рис.1.29) и дополнительные свойства пространства и времени, запишем преобразования Галилея:

Переход из К´ в К : Переход из К в К ^': (1.88)

В заключение параграфа отметим важный принцип, существенно упрощающий описание механических явлений в разных ИСО. Это принцип относительности Галилея, он является следствием опытных фактов и утверждает равноправие всех ИСО по отношению к происходящим в них механически явлениям. Приведем различные эквивалентные формулировки этого принципа относительности: 1) никакими механическими опытами, находясь внутри ИСО, нельзя установить, движется она равномерно и прямолинейно или покоится; 2) все законы механики выглядят, записываются одинаково во всех ИСО; 3) все механические явления протекают одинаково во всех ИСО; 4) все законы механики инвариантны относительно преобразований Галилея.

Под инвариантной величиной понимают величину, принимающую одинаковое значение во всех ИСО. Под инвариантной формулой понимают формулу, которая записывается одинаково во всех ИСО.

Покажем, что второй закон Ньютона инвариантен относительно преобразований Галилея, т.е. он записывается одинаково во всех ИСО:

С.О. К: F=ma, С.О. К^': F’=m'a'.

Для этого рассмотрим, как преобразуются масса и ускорение при переходе из одной системы отсчета в другую. В классической механике масса тела является инвариантной величиной (m=m’), ход времени во всех ИСО одинаков (t=t’) и закон сложения скоростей выглядит таким образом

(1.89)

где считается, что тело движется в С.О. К и К' со скоростями и ; направленными вдоль осей Ох и О'х' . Тогда можно записать:

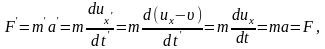
что и требовалось показать.