1.4.8. Применение законов сохранения импульса и механической энергии к анализу абсолютно упругого и неупругого столкновений

Как уже отмечалось ранее, законы сохранения позволяют получить важную информацию о взаимодействии тел без детального решения второго закона Ньютона. Рассмотрим ряд важных для практики примеров.

1. Абсолютно неупругий удар – это удар, в результате которого тела после соударения движутся вместе как единое целое. Пусть движущееся со скоростью тело массы m₁ сталкивается с движущимся со скоростью телом массы m₂, в результате чего их скорость оказывается равной (рис.1.27)

Если эти тела образуют замкнутую систему, то для нее можно записать закон сохранения импульса

,

из которого следует, что скорость тел после удара будет равна

. (1.84)

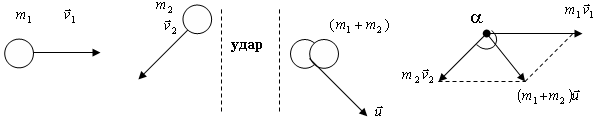
Рис.1 27

При таком ударе возникают неконсервативные силы (силы сопротивления), которые переводят часть механической энергии соударяющихся тел в тепловую энергию

, (1.85)

г де угол a в выражениях (1.84) и (1.85) – угол между векторами и .

В качестве примера рассмотрим взаимодействие молота (масса m₁, скорость его в момент удара ) и наковальни (масса m₂>>m₁, =0) при ковке куска металла. Из формул (1.84) и (1.85) получим

. (1.86)

Как следует из выражения (1.86), КПД h удара тем выше, чем больше различие в массах наковальни и молота. В этом случае большая доля механической энергии молота переходит во внутреннюю энергию куска металла, идет на его деформацию.

2. Абсолютно упругий центральный удар – это удар, при котором помимо закона сохранения импульса, выполняется также и закон сохранения механической энергии. При таком ударе деформации тел, возникающие в момент соударения, после столкновения полностью исчезают. При центральном ударе тела до и после соударения движутся по одной прямой.

Пусть движущееся вдоль оси Ох со скоростью тело массы m₁ сталкивается с движущимся вдоль ( > ) или против оси Ох со скоростью телом массы m₂, в результате чего их скорости оказываются равными и (рис.1.28). Используя для замкнутой системы, состоящей из двух тел, законы сохранения импульса и механической энергии, найдем проекции скоростей и тел на ось Ох после их соударения

(*)

. (**)

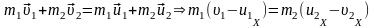Учитывая выражение (**), можно упростить формулу (*)

.

П одставляя в (**), получим:

. (1.87)

Рис.1.28

Рассмотрим ряд важных для практики частных случаев использования формул (1.87)

Пример 1. Два тела одинаковой массы ( ), движущиеся вдоль оси ох со скоростями и ( > ).навстречу друг другу ( , ) и испытывают упругое соударение, в результате которого согласно формул (1.87) происходит обмен их скоростями: , . При =0 получим, что скорость первого тела за одно соударение снизится до нуля: .

В ядерных реакторах необходимо проводить эффективное уменьшение скорости нейтронов, возникающих при реакциях деления, от скоростей порядка 1×10⁷ м/с до скоростей, соответствующих скорости их теплового движения при температуре Т=300 К (»3×10³ м/с). Как следует из рассмотренного примера, для этого необходимо заставить нейтроны испытывать соударения с близкими по массе атомами водорода, входящими в состав воды Н₂О (скорость атомов водорода можно считать практически равной нулю по сравнению со скоростью нейтронов). Однако из-за большой потери нейтронов, связанных с протеканием при таких столкновениях реакций образования атомов тяжелого водорода ( H), используют в качестве замедлителя тяжелую воду (D₂O). При этом требуется порядка 10 столкновений для требуемого замедления скорости нейтронов.

Пример 2. Тело массы m₁, движущееся со скоростью , упруго ударяется о неподвижное тело, масса которого существенно больше m₁ ( =0, m₂ >> m₁ ). Согласно формулам (1.87) после столкновения первое тело будет двигаться в обратном направлении с той же по модулю скоростью, а второе тело практически останется неподвижным ( , ). Такое столкновение происходит при лобовом ударе молекулы о стенку сосуда. При этом молекула упруго (без потери скорости) отскакивает обратно, а стенка остается практически неподвижной. Результаты такого столкновения молекулы со стенкой сосуда используются при выводе основного уравнения молекулярно-кинетической теории для давления идеального газа.

Если же стенка (поршень) будет двигаться вдоль оси ох cо скоростью , то, как следует из формул (1.87), в результате столкновения молекула теряет часть своей скорости ( ), а скорость поршня останется неизменной ( ). Это означает, что расширение газа, возникающее при движении поршня, в отсутствие теплопередачи (отсутствуют внешние источники увеличения средней скорости теплового движения молекул) приводит к его охлаждению (средние скорости движения молекул уменьшаются), так как работа газа происходит за счет уменьшения его внутренней энергии.

Лекция 7