36,37. Упругое дифференцирующее(интегрирующее) звено, его характеристики
Упругое звено описывается дифференциальным уравнением вида
.
Примерами упругого звена (см. рис. III. 33) могут служить пассивные четырехполюсники вида
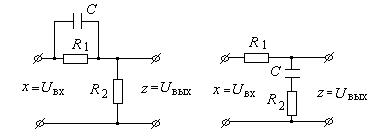
Рис. III. 33. Примеры упругого звена.
Характеристики
упругого звена существенно зависят от
параметра 
.
При λ >
1, т.е. при Т0 > T звено
называется упругим дифференцирующим,
в противном случае, при λ <
1 – упругим интегрирующим.
Легко понять, что для упругого дифференцирующего звена (λ > 1) h(0) > h( ∞), а для упругого интегрирующего звена (λ < 1) h(0) < h( ∞). В соответствии с этим зависимости h(t) для λ > 1 и λ < 1 примет вид, изображенный на рис. III. 34 а, в
а) λ >1 в) λ < 1
Рис. III. 34. Переходная характеристика упругого звена.
Весовая функция звена может быть определена из соотношения
.
Видно,
что весовая функция (рис. III. 35) состоит
из двух составляющих – первая 
-
это δ –
функция площадью kλ,
проходящая по оси ординат, и
вторая 
существует
для всех t ≥
0. Кроме того, из последнего выражении
можно усмотреть, что весовая функция w(t)
упругого звена зависит от
параметра λ. Следовательно,
графики w(t)
дифференцирующего (λ >1)
и интегрирующего (λ <1)
упругих звеньев (рис. III. 35 а, б) будут
иметь различный вид
а) λ >1 в) λ < 1
Рис. III.35. Весовая функция упругого звена.
Частотная передаточная функция звена, исходя из (III.1.22), имеет вид
.
Следовательно,
амплитудная частотная A(
)
фазовая частотная φ(
)
характеристики могут быть представлены
следующим образом
а) в) с)
Рис. III.36. A( ), φ( ) и w( ) упругого дифференцирующего звена (λ > 1).
а) в) с)
Рис. III.37. A( ), φ( ) и w( ) упругого интегрирующего звена (λ < 1).
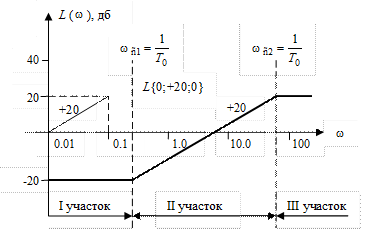
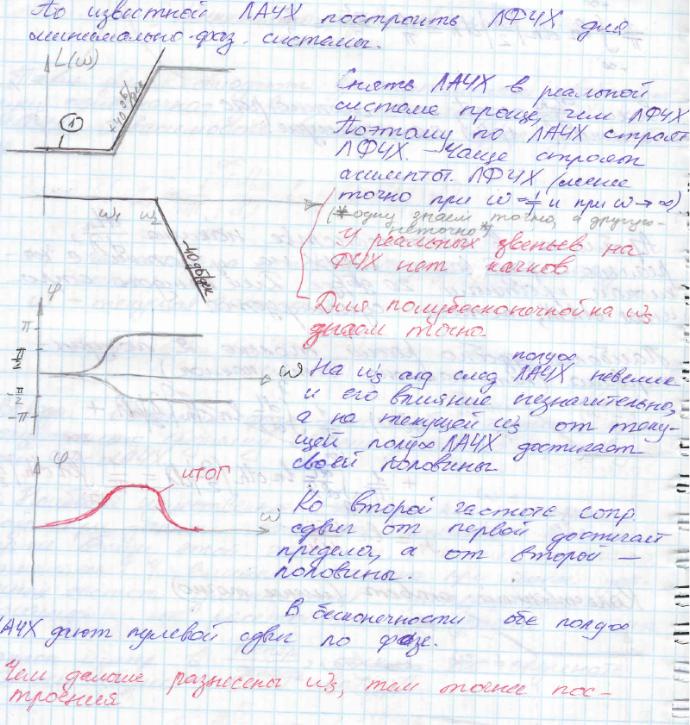
38,39,40)Минимально-фазовые системы, их свойства.
