19. Обобщенная структурная схема системы в динамике.

Система автоматического управления (рис 1.1) содержит: устройство управления (УУ) или регулятор, на вход которого подается задающее воздействие (входной сигнал или совокупность сигналов)  х_вх(t).Задающее воздействие определяет требуемый закон управления. В результате этого воздействия на выходе регулятора вырабатывает управляющее воздействие U(t), которое поступает на вход объекта управления (ОУ).

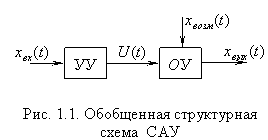
Под ОУ в данном курсе понимается любое техническое устройство (станок, самолет, турбина и т.д.), для функционирования которого необходимы специально организованные воздействия U(t). Качество управления оценивается по значению выходной величины объекта х_вых(t) – это обычно главный технологический параметр (скорость, мощность, производительность и т.д.).

Наряду с х_вх(t),  внешним по отношению к рассматриваемой САУ являются  возмущающее воздействие х_возм(t), которое,  как и U(t), приложено к ОУ. К числу таких возмущений можно отнести  момент сопротивления при металлообработке, колебание напряжения в сети, ветровую нагрузку и т.д. Возмущающие воздействия искажают требуемый закон управления. Очевидно, что в первом приближении задача синтеза САУ состоит в разработке такого УУ, с которым и при наличии существенных возмущающих воздействий отклонение требуемого закона управления ОУ от фактического не превышает допустимых значений.

20. Связь между передаточной функцией замкнутой и разомкнутой системы.

Типовая структура замкнутой САУ, передаточная функция и характеристическое уравнение разомкнутой системы.

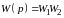– передаточная функция разомкнутой системы.

Для линейных систем применим принцип суперпозиции воздействий (независимых воздействий).

- Передаточная функция замкнутой системы относительно регулирующей величины по задающему воздействию.

– передаточная функция замкнутой системы относительно задающей величины по возмущающему воздействию.

– передаточная функция замкнутой системы относительно ошибки регулирования, по задающему воздействию.

– передаточная функция замкнутой системы относительно ошибки регулирования, по возмущающему воздействию.

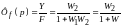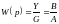– передаточная функция разомкнутой системы.

21) Комплексные коэффициенты передачи (ККП). Определение.

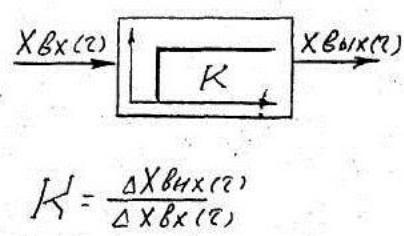
вых(η) / Хвх(η)=К , Хвых(η), Хвх(η) ‒ изменение вых. и вх. параметра во времени;

К ‒ коэффициент передачи (усиления) звена.

К показывает, на сколько изменится выходная величина при изменении входной на еди-ницу. Необходимо помнить, что размерности Хвых(η) и Xвx(η). как, правило, не совпадают.

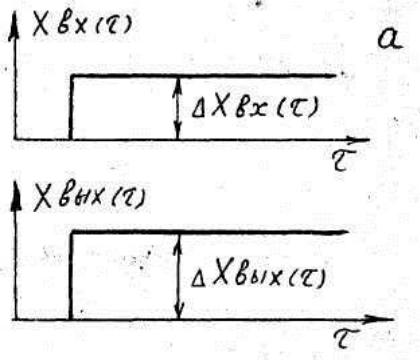
На рис.1 показано условное обозначение пропорцио-нального звена и траектории изменения во времени Хвых(η) и Хвх(η).

22) Связь между ККП и передаточной функцией.

23) Амплитудно-частотные характеристики . Определение. Пример.

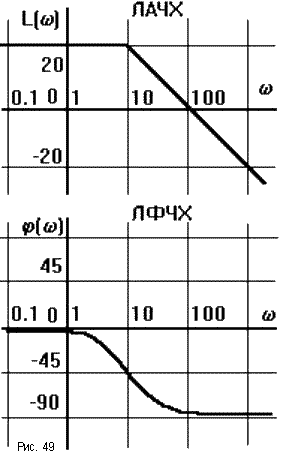
АЧХ дает отношение амплитуд выходного и входного сигналов. Зависимость отношения амплитуд от частоты называют амплитудной частотной

характеристикой А(ω).

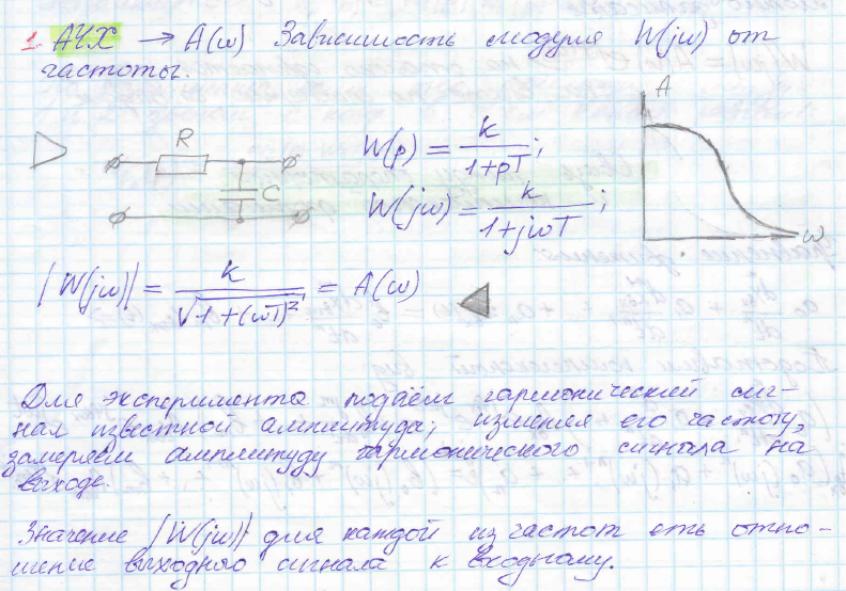
Пример: Интегрирующее звено

АЧХ: A( ) = 1/ .

АЧХ представляет собой прямую, проходящую через точку L( ) = 0 при = 1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон АЧХ равен - 20 дб/дек (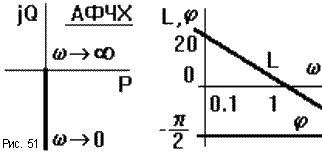 децибел на декаду).

24) Фазо-частотные характеристики . Определение. Пример.

ФЧХ - сдвиг по фазе выходной величины относительно входной. Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой θ(ω). ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси .

25) Амплитуд –фазовые частотные характеристики . Определение. Пример.

Если W(j ) изобразить вектором на комплексной плоскости, то при изменении от 0 до + его конец будет вычерчивать кривую, называемую годографом вектора W(j ), или амплитудно - фазовую частотную характеристику (АФЧХ) (рис.48). Ветвь АФЧХ при изменении от - до 0 можно получить зеркальным отображением данной кривой относительно вещественной оси.

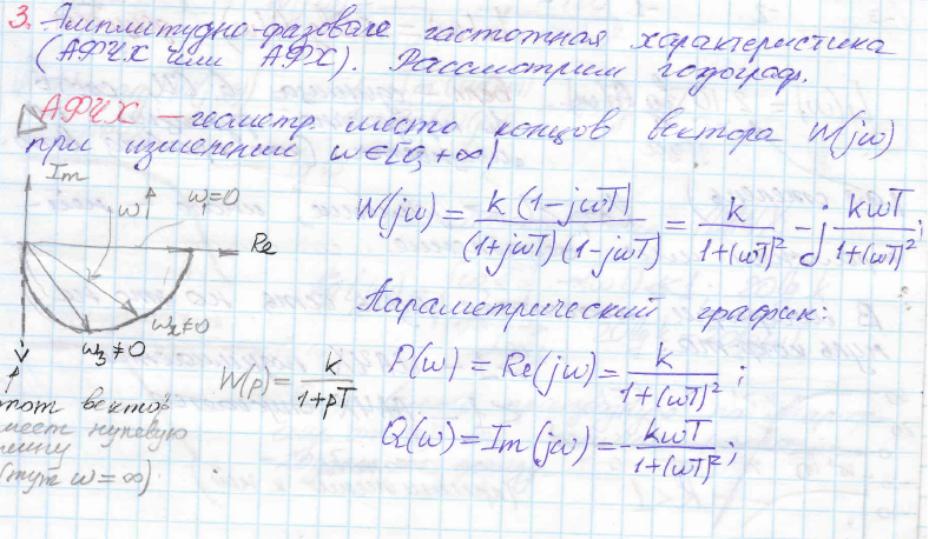
Пример: Интегрирующее звено

АФЧХ: W(j ) = .

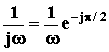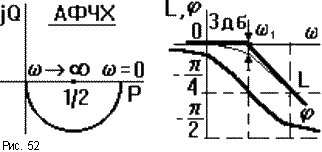
26) Логарифмические характеристики . Пример.

В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) (рис.49): логарифмическая амплитудная ЧХ (ЛАЧХ) L( ) и логарифмическая фазовая ЧХ (ЛФЧХ) ( ). Они получаются путем логарифмирования передаточной функции:

ЛАЧХ получают из первого слагаемого, которое из соображений масштабирования умножается на 20, и используют не натуральный логарифм, а десятичный, то есть L( ) = 20lgA( ). Величина L( ) откладывается по оси ординат в децибелах. Изменение уровня сигнала на 10 дб соответствует изменению его мощности в 10 раз. Так как мощность гармонического сигнала Р пропорциональна квадрату его амплитуды А, то изменению сигнала в 10 раз соответствует изменение его уровня на 20дб,так как

lg(P₂/P₁) = lg(A₂²/A₁²) = 20lg(A₂/A₁).

По оси абсцисс откладывается частота w в логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соответствует изменение w в 10 раз. Такой интервал называется декадой. Так как lg(0) = - , то ось ординат проводят произвольно.

ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси . Величина ( ) откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: - + .

ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно восстановить ее передаточную функцию и определить параметры.

Пример: Интегрирующее звено

27) Построение асимптотической логарифмической амплитудно-частотной хар. Пример.

Для построения ЛАЧХ и ЛФЧХ рекомендуется следующий порядок:

1) раскладывают сложную передаточную функцию на множители, являющиеся передаточными функциями типовых динамических звеньев (порядок полиномов числителя и знаменателя не выше второго);

2) вычисляют сопрягающие частоты отдельных звеньев и строят асимптотические ЛАЧХ и ЛФЧХ каждого элементарного звена;

3) путем графического суммирования ЛАЧХ и ЛФЧХ звеньев строят результирующие ЧХ.

Рассмотрим конкретный пример:

W(p) = 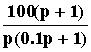= W₁W₂W₃W₄. 

Раскладываем данную передаточную функцию на передаточные функции элементарных звеньев:

1) безынерционное звено: W₁ = K₁ = 100 => L(w) = 20lg100 = 40; 

2) форсирующее звено:W₂ = p + 1;  его параметры: K₂ = 1, T₂ = 1, ₂ = 1/T₂ = 1; 

3) интегрирующее звено: W₃ = 1/p;  его ЛАЧХ проходит через точку L = 0 при частоте = 1;

4) апериодическое звено:W₄ = 1/(0.1p + 1);  его параметры: K₄ = 1, T₄ = 0.1, ₄ = 1/T4 = 10.

П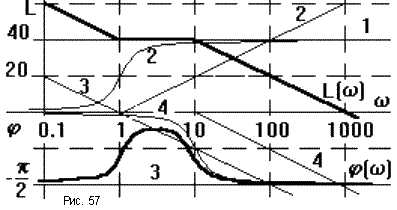 орядок построения ЛАЧХ и ЛФЧХ показан на рис.57.

28) Переходная характеристика. Определение . Пример.

29) Связь между переходной характеристикой и передаточной функцией.

теоретически.

30) Частный случай теоремы разложения. Отсутствуют кратные и нулевые корни.

30. Частный случай теоремы разложения. Отсутствуют кратные и нулевые корни.

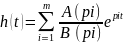pi – корни B(p)=0

p(1+pT)=0 -> p1=-

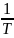
31. Частный случай теоремы разложения. Существует один нулевой корень.

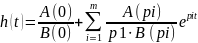
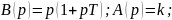
32. Типичные звенья линейных САП.

1. Безынерциальные звенья W(p)=k

Не искажает сигнал, постоянная передаточная характеристика. Аналог – резистивный делитель.

2. Инерционное звено.

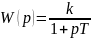
Генератор постоянного тока, RC – соединение.

Определение постоянных времени:

А) по переходной характеристике: h(T)=0.63k

Б) по АФХ

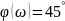
На высокой частоте звено разрывает, сдвиг сигнала π/2 по фазе.

3. Интегрирующее звено

В статике при огромном коэффициенте исчезают ошибки. Действие схоже с инерционным звеном.

4. Дифференциальное звено. W(p)=pT

Трудно найти аналог.

5. Упругие звенья. Дифференцирующее Т1>T2 и интегрирующее T2>T1

Упругое, потому что появляется в узком диапазоне частоты.

6. Колебательное звено.

Для колебаний нужно минимум 2 объекта, в которых может запасаться энергия

3 3. Инерциальное звено, его характеристики

Инерционное звено первого порядка описывается уравнением:

.                           

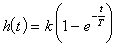
Его переходная функция (кривая разгона):

Импульсная функция:

.                         

Кривая разгона и импульсная переходная функция инерционного звена первого порядка приведены соответственно на рис. 30 и 31.

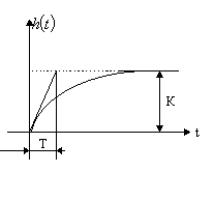
Рис. 30. Кривая разгона инерционного звена первого порядка Рис. 31. Импульсная переходная функция