13. Передаточная функция. Определение. Связь между уравнением движения и передаточной функцией.

В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператора p = d/dt так, что, dy/dt = py. В операторной форме исходное дифференциальное уравнение записывается как алгебраическое: 

a_op⁽ⁿ⁾y + a₁p^(n-1)y + ... + a_ny = (a_op⁽ⁿ⁾ + a₁p^(n-1) + ... + a_n)y = (b_op^(m) + b₁p^(m-1) + ... + bm)u

Оператор p можно рассматривать в качестве сомножителя без права перестановки, то есть py yp. Его можно выносить за скобки и т.п.

Поэтому уравнение динамики можно записать также в виде:

 

 

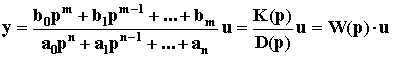
Дифференциальный оператор W(p) называют передаточной функцией. Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/u(t), поэтому ее еще называют динамическим коэффициентом усиления. В установившемся режиме d/dt = 0, то есть p = 0, поэтому передаточная функция превращается в коэффициент передачи звена K = b_m/a_n.

Знаменатель передаточной функции D(p) = a_opⁿ + a₁p^{n - 1} + a₂p^{n - 2} + ... + a_n называют характеристическим полиномом. Его корни, то есть значения p, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функции.

Числитель K(p) = b_op^m + b₁p^{m - 1}+ ... + b_m называют операторным коэффициентом передачи. Его корни, при которых K(p) = 0 и W(p) = 0, называются нулями передаточной функции.

14. Способы определения передаточной функции.

Передаточной функцией W(p) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.

Допустим динамика описывается дифференциальным управлением:

Применим к данному уравнению прямое преобразование Лапласа:

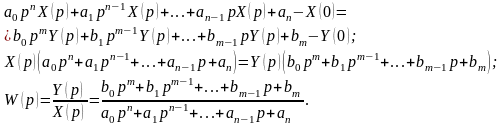
15. Структурный метод анализа сар. Звено направленного действия.

При исследовании систем управления первостепенное значение приобретает характер преобразования сигналов в отдельных элементах, или звеньях. Динамические системы, передаточные функции которых имеют вид простых дробей, называются типовыми или элементарными звеньями. Любой промышленный объект представляется в виде связанных между собой типовых звеньев. Их основу составляет звено направленного действия, основное свойство которого заключается в том, что выходная величина y(t) зависит от входной величины x(t), но обратное воздействие выхода на вход отсутствует. Присоединение к выходу такого звена другого звена не изменяет передаточной функции первого звена. Физическая природа звена направленного действия может быть любой. Характеризуется оно соответствующим уравнением движения, которое и определяет конкретный тип элементарного звена.

Различают следующие звенья: усилительное, интегрирующее, идеальное и реальное дифференцирующие, форсирующее, чистого запаздывания, инерционно-форсирущее, апериодические первого и второго порядка, колебательное, которые по ряду общих закономерностей можно разделить на следующие группы:

1 Статические звенья, у которых статическая характеристика отлична от нуля, имеют однозначную связь между входной и выходной переменными в статическом режиме. К ним относят усилительное, апериодическое, колебательное звенья, у которых передаточный коэффициент связан с передаточной функцией соотношением k = W ( s ) s = 0 . Кроме того, статические звенья являются фильтрами низкой частоты, исключение составляет усилительное звено.

2 Дифференцирующие звенья, у которых статическая характеристика равна нулю, – это идеальное и реальное дифференцирующие звенья; в их передаточную функцию всегда входит сомножитель s, поэтому W ( s) s = 0 = 0 . Дифференцирующие звенья являются фильтрами высокой частоты, они вносят положительные фазовые сдвиги.

3 Астатические звенья – звенья, не имеющие статической характеристики, к ним относится интегрирующее звено, в передаточную функцию которого обязательно входит сомножитель