
- •10 Вопрос делимость в кольце целых чисел
- •12.Алгоритм Евклида (нахождение наибольшего общего делителя)
- •Описание алгоритма нахождения нод делением
- •13.Бином Ньютона
- •Свойства бинома Ньютона
- •14. Сравнения по модулю m.
- •18. Планарный граф
- •Простейшие свойства плоских графов Формула Эйлера
- •Два примера непланарных графов Полный граф с пятью вершинами[
- •«Домики и колодцы»[править | править исходный текст]
- •Теорема Понтрягина — Куратовского
- •22. Взвешенные графы
- •23. Соответствие и функции Соответствия
- •Отображения и функции
- •Верхняя и нижняя грани множества
- •30. Матрица как линейный оператор.
- •33. Виды и способы задания графов
- •34 Корректно поставленная задача
- •Конечные и бесконечные множества.
- •40. Компоненты связности, следствия.
- •43. Примеры норм матриц
- •Степени вершин и обходы графов
- •Обход графа в глубину
- •Обход графа в ширину
- •46. Перечислите шаги алгоритма Дейкстры
- •49. Основные компоненты параметризованного синтеза в системах
- •51. Что выделяет функцию из трех известных бинарных отношений
- •Примеры среды систем как линейных метрических пространств
- •Классификация множеств по мощности
- •Каковы основные этапы построения полного оптимального потока в ориентированном графе(Форда-Фалкерсона).
43. Примеры норм матриц
Нормой
матрицы
![]() называется
вещественное
число
называется
вещественное
число
![]() ,
удовлетворяющее первым
трём из
следующих условий:
,
удовлетворяющее первым
трём из
следующих условий:
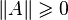 ,
причём
,
причём
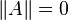 только
при
только
при
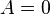 ;
;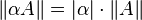 ,
где
,
где
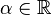 ;
; ;
;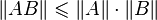 .
.
Если выполняется также и четвёртое свойство, норма называется субмультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы субмультипликативны.
Матричная
норма
![]() из
из
![]() называется
согласованной с векторной нормой
называется
согласованной с векторной нормой
![]() из
из
![]() и
векторной нормой
и
векторной нормой
![]() из
из
![]() если
справедливо:
если
справедливо:
![]()
для
всех
![]() .
.
Пример: Любое предгильбертово пространство можно считать нормированным, так как скалярное произведение порождает естественную норму
Степени вершин и обходы графов
Степень вершины (англ. degree,
также валентность, англ. valency)
в теории
графов — количество
рёбер графа
![]() ,
инцидентных
вершине
,
инцидентных
вершине
![]() .
При подсчёте степени ребро-петля
учитывается дважды.[1]
Степень вершины обозначается как
.
При подсчёте степени ребро-петля
учитывается дважды.[1]
Степень вершины обозначается как
![]() (в
западных источниках —
(в
западных источниках —
![]() ).
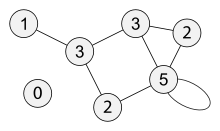
Максимальная и минимальная степень
вершин графа G обозначаются соответственно
Δ(G) и δ(G). На рис. 1 максимальная
степень равна 5, минимальная — 0. В
регулярном
графе степени всех вершин
одинаковы, поэтому в данном случае можно
говорить о степени графа.
).
Максимальная и минимальная степень
вершин графа G обозначаются соответственно
Δ(G) и δ(G). На рис. 1 максимальная
степень равна 5, минимальная — 0. В
регулярном
графе степени всех вершин
одинаковы, поэтому в данном случае можно
говорить о степени графа.
Общие свойства
Если все вершины графа имеют одинаковую степень k, граф называют k-регулярным или регулярным графом степени k. В этом случае сам граф имеет степень k.
Эйлеров путь существует в неориентированном, связном графе если и только если граф имеет 0 или 2 вершины нечётной степени. Если граф содержит 0 вершин нечётной степени, Эйлеров путь является циклом.
Орграф является псевдолесом только если полустепень захода каждой вершины не больше 1. Функциональный граф — частный случай псевдолеса, в котором полустепени захода всех вершин равны 1.
Согласно теореме Брукса, хроматическое число любого графа за исключением клики или нечётного цикла не превышает максимальной степени его вершин (Δ). Согласно теореме Визинга, хроматический индекс любого графа не превышает Δ + 1.
k-вырожденным графом называется граф, в котором каждый подграф имеет вершину степенью не больше k.
Обход графа в глубину
На каждом шаге поиска в глубину алгоритм выбирает новую вершину, смежную с текущей и продолжает поиск уже из нее. Такое «углубление» продолжается до тех пор, пока не будет найдена вершина, смежная с конечной или алгоритм не зайдет в тупик. Функция возвращает пару (результат, путь), где результат представляет собой флаг, показывающий наличие пути.
В результате рекурсивного вызова (п. 3.2) может быть найден путь, проходящий через одну из смежных со Start дуг. Если путь найден — то его необходимо дополнить соответствующей дугой (п.3.3), в противном случае — перейти к поиску пути, проходящему через другую дугу (п. 3.4).
Стоит отметить, что на шаге 3 алгоритма листинг 1 выбирается произвольная дуга, однако, выбор дуга влияет на результат, т.к. алгоритм не гарантирует что найденный путь будет кратчайшим. Например, если при поиске пути из вершины P а вершину F, первой будет выбрана дуга (P, D), то будет найден путь (P, D, F), однако, если первой будет взята дуга (P, B), то может быть найден путь (P, B, C, D, F).
