12.Закони комутації. Перехідний, вимушений та вільний режими.

Перехідний, вимушені і вільні процеси

Розглянемо спочатку деякі загальні питання розрахунку пере­хідних процесів на прикладі включення нерозгалуженого ланцюга з опором, індуктивністю і ємкістю (послідовного контура) до джерела ерс е, яка змінюється в часі безперервно і задана яким-небудь аналітичним виразом.

Запишемо другий закон Кірхгофа для будь-якого моменту часу:

^(12.1)

де і — струм перехідного процесу, який надалі називатимемо перехідним струмом або просто струмом і.

Коли з перехідним процесом можна вже не вважатися, настає вимушений режим. Вимушений режим, що створюється джерелом довільною періодично змінюючої ерс (або струму), називають ще сталим режимом. Після закінчення перехідного процесу джерело ерс, що змінюється, наприклад, по експоненціальному закону, створює вимушений режим, а джерело постійної ерс або ерс, що змінюється по гармонійному закону, створює вимушений або усталений режим.

Коли наступить вимушений режим, рівняння (12.1) прийме вигляд:

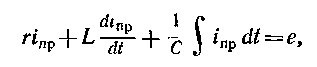^(12.2)

де і_пр — струм вимушеного режиму або просто вимушений струм. Віднімаючи почленно рівняння (12.2) з рівняння (12.1) і позначаючи

(12.3), отримуємо:

^(12.4)

або:

^(12.5)

Різниці струмів і напруги перехідного процесу і вимушеного режимів називаються відповідно струмом і напругою вільного процесу або просто вільним струмом і напругою.

Рівняння (12.4) показує, що під час переходу ланцюга від одного вимушеного стану до іншого напруга на всіх елементах, що створюється вільними складовими струмів, взаємно зрівноважуються, але вільна напруга залежить, звичайно, від ерс джерела.

Рівняння (12.3) показує, що процес, що відбувається в ланцюзі, можна розглядати таким, що складається з двох процесів, що накладаються один на одного, — вимушеного, який як би насту­пив відразу, і вільного, такого, що має місце тільки під час пере­хідного процесу. Завдяки вільним складовим і дося­гаєтся в перехідному процесі безперервне наближення до вимушеного режиму. Отже, під час перехідного процесу струми і напруга можуть бути розкладені на тих, що складають вимушений і вільний режими:

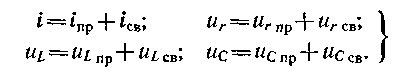^(12.6)

Оскільки принцип накладання застосовний лише до лінійних ланцюгів, то це розкладання допустиме для лінійних ланцюгів Звичайно, фізи­чно існують тільки перехідні струми і напруга і розкладання їх на вимушені і вільні складові є зручним математичним прийомом, що полегшує розрахунок перехід­них процесів в лінійних ланцюгах.

Розкладання перехідних струмів і напруги відповідає правилу вирішення лінійних неоднорідних диференціальних рівнянь, згідно якому загальне вирішення таких рівнянь дорівнює сумі часткового вирішення неоднорідного рівняння і загального рішення однорідного рівняння.

Дійсно, вільний струм є загальним рішенням однорідного диференціального рівняння (12.4) і, відповідно, в його виразі мають бути сталі інтегрування, число яких дорівнює порядку диференціального рівняння.

Вимушеним струмом є частковим вирішенням неод­норідного диференціального рівняння (12.1), а саме таке, яке виходить із загального вирішення неоднорідного диферен­ціального рівняння при рівних нулю сталих інтегрування. Іншими словами, у складі вимушеного струму не повинно бути складових вільного струму. Тоді перехідний струм і, рівний сумі i_пр і i_св (12.6), і буде загальним вирішенням того ж самого неоднорід­ного диференціального рівняння.

За допомогою законів комутації неважко знайти початкові значення вільного струму в вітках з індуктивністю i_Lсв(0) і вільної напруги на ємності u_Ссв(0), що необхідне для визначення сталих інтегрування.

Нехай ланцюг до комутації знаходився в довільному режимі. Позначимо струм і напругу цього режиму і_L(t) i u_c (t) . У момент комутації t= 0 cтрум і напруга режиму до комутації вважатимемо відомими. Оскільки перехідний струм в індуктивності і перехідна напруга на ємності у момент комутації не можуть змінюватися стрибком, то на підставі (12.6) маємо:

або:

Якщо ланцюг до комутації знаходився в вимушеному режимі, то, позначаючи струм і напругу цього режиму і отримуємо:

У окремому випадку, коли до комутації ланцюг був відключений і на ємності не було заряду, тобто і маємо:

Перший закон (правило) комутації. Струм через індуктив­ний елемент L безпосередньо до комутації i_L(0_) дорівнює струму через цей же індуктивний елемент безпосередньо після комму­тации i_L(0₊);

^(12.7)

Час t = 0_ є часом безпосередньо до комутації, t = 0₊ — після комутації. Рівність (12.7) виражає собою перший закон комутації.

Другий закон (правило) комутації. Позначимо напругу на конденсаторі безпосередньо до комутації u_с(0_), а напруга на ньому безпосередньо після комутації u_c(0₊).

Відповідно до неможливості стрибка напруги на кон­денсаторі:

^(12.8)

Рівність (12.8) виражає собою другий закон комутації.