18.Закон повного струму.

Інтегральна форма закону повного струму. Кількісний зв'язок між циркуляцією вектора по замкнутому контуру і струмом усередині контура визначається законом повного струму в інтегральній формі — лінійний інтеграл від напруженості магнітного поля уздовж будь-якого замкнутого контура дорівнює повному струму, пронизуючи замкнутий контур:

(18.1)

Під повним струмом розуміють весь струм (струм провідності і струм зміщення), який проходить через контур інтегрування.

Інтегральну форму закону повного струму застосовують, коли може бути використана симетрія в полі. Так, наприклад, напруженість поля в деякій точці А в полі відокремленого прямого дроту із струмом І (рис. 18.1) за законом повного струму визначають таким чином. Проведемо через точку А коло радіусом R в площині, перпен­дикулярної осі дроту, так що центр її знаходиться на цій осі. У си­лу симетрії напруженість поля в усіх точках кола чисельно одна і та ж. Напрям напруженості збігається з дотичною до кола. Тому:

Із збільшенням радіусу R напруженість магнітного поля змінюється по гіперболічному закону.

Якщо яке-небудь поле має складний характер і не вдається утворити замкнутий контур, всі точки якого знаходилися б в симетрич­них умовах, то хоча інтегральна форма запису закону повного струму справедлива і для такого контура, використовувати її для знаходження напруженості в будь-якій точці поля так просто не вдається.

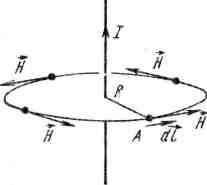
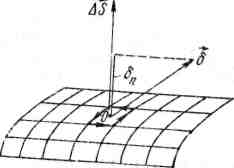
Рисунок. 18.1 Рисунок. 18.2

Диференціальна форма закону повного струму. Співвідношення (18.1) використовується для контура будь-яких розмірів, у тому числі і для дуже малого.

Виділимо в якому-небудь середовищі невеликий контур («жирно» обведений на рис. 18.2) складемо уздовж нього циркуляцію вектора Н. Циркуля­ція напруженості поля вздовж цього контура дорівнює струму, що проходить обведену площу.

Якщо площа мала, то можна вважати, що щільність струму  в межах цієї площі однакова і тоді струм, пронизуючий пло­щу . Тут — проекція вектора щільності струму на нормаль до площі, тобто на напрям

За позитивний напрям нормалі до площі приймають на­прям руху вістря правого гвинта, головка якого обертаєть­ся в напрямі, прийнятому за позитивне при обході контура і складанні циркуляції.

Розділимо обидві частини рівності на S і спрямуємо S до нуля. Це бу­де відповідати стяганню даної площі до нуля. Межа отриманого відношення:

.

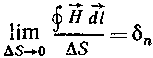У лівій частині рівності знаходиться величина, що є проек­цією ротора на напрям нормалі до площі . Отже .

Якщо площу S орієнтувати в просторі так, що напрям нормалі до неї збіжиться з напрямом вектора щільності струму в даній точці поля, то тоді замість рівності проекцій двох векто­рів можна записати рівність самих векторів:

(18.2)

Формула (18.2) і є законом повного струму в дифе­ренціальній формі.

Ротор — це функція, що характеризує поле в даній точці відносно здібності до утворення вихорів.

Рівняння (18.2) записане в загальній формі безвідносно до си­стеми координат, і в кожній конкретній системі координат воно роз­криваєтся по-своєму.

19.Рівняння Максвела для змінного електромагнітного поля.

При дослідженні процесів в змінному електромагнітному полі користуються рівняннями Максвелла.

Систему рівнянь Максвелла утворюють чотири рівняння:

1) рівняння (22.1), що виражає зв'язок між ротором напруженості магнітного поля і щільністю струму в тій же точці поля, - перше рівняння Максвелла;

2) рівняння (22.4), яке визначає зв'язок між ротором на­пруженості електричного поля і швидкістю зміни магнітного поля в тій же точці поля, — друге рівняння Максвелла;

3) рівняння , що виражає принцип безперервності магнітного потоку [воно виходить з (22.4) після узяття від обох частин його дивергенції];

4) рівняння , що виражає зв'язок між витоком напруженості електричного поля і щільністю вільних зарядів в тій же точці поля.

Цю систему доповнюють рівнянням безперервності і теоремою Умова — Пойнтінга.

Перше рівняння Максвел­ла записують таким чином:

(22.1)

У правій частині його є дві щільності струму: щільність струму провідності  і щільність струму електричного зсуву . Струм електричного зсуву виникає в будь-якому діелектрику, у тому числі і у вакуумі, при зміні напруженості електричного поля в часі. Струм зсуву породжує магнітне поле так само, як і струм провідності. Хоча природа струму провідності і струму зсуву не­ однакова, обидва вони володіють однією і тією ж властивістю — викликати магнітне поле.

Таким чином, сенс першого рівняння Максвелла полягає в тому, що всяка зміна електричного зсуву в часі в деякій точці поля (тобто виникнення в ній струму зсуву) на таких же правах, як і струм провідності, викликає в цій точці вихор магнітного поля , тобто викликає вихрове магнітне поле. Якщо середовище однорідне і ізотропне, то і тоді:

Із струмом зсуву в попередніх розділах доводилося зустрічатися неодноразово. Так, відомо, що при заряд­ці конденсатора через нього протікає струм. Цей струм протікає через діелектрик і є струмом зсуву.

Якщо, наприклад, узяти незаряджений плоский повітряний конден­сатор і підключити його до джерела ерс. напругою U через опір R, то напруга на обкладаннях конденсатора ростиме згідно із законом . Оскільки напруженість електричного поля в плоскому конденсаторі , де d — відстань між обкладаннями, то . Ємність плоского конденсатора .

Струм зсуву, що протікає через одиницю поверхні перетину діелектрика, узятої перпендикулярно силовим лініям:

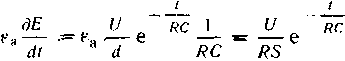
Через поверхню S струм зсуву в S разів більший, тобто він дорівнює струму провідності, що протікає по провідниках, з’єднуючим кон­денсатор з джерелом ерс.

Відзначимо, що перше рівняння Максвелла є за­кон повного струму в диференціальній формі.

Переконаємося в тому, що із закону повного струму виходить рівняння (22.1). З цією метою візьмемо довільний контур і складемо для нього рівняння за законом повного струму. Повний струм, що проходить через площу, обмежену контуром, дорівнює сумі струму провідності і струму зсуву. Тому:

На підставі теореми Стокса . Отже:

(22.2)

Рівність (22.2) повинна виконуватися при будь-якій площі S, тому:

Рівняння безперервності. Лінії повного струму є безперервними. Фізично це означає, що на межі провідного середовища і діелектрика струм провідності переходить в струм зсуву.

Можна математично сформулювати принцип безперервності (замкнутості) ліній повного струму. З цією метою від обох частин рівняння (22.1) візьмемо дивергенцію. З попереднього відомо, що ди­вергенція від ротора тотожно дорівнює нулю. Тому

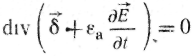(22.3)

Рівняння (22.3) можна записати в іншій формі. Дійсно, з нього виходить, що Тому:

(22.3а)

Рівняння безперервності (22.3а) називають також законом збереження заряду. Цей закон означає, що електричний заряд незнищенний, він може тільки переміщатися з одного місця в інше.

Друге рівняння Максвелла. Друге рівняння Максвел­ла записують таким чином:

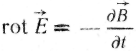(22.4)

Фізичний сенс його полягає в тому, що всяка зміна магніт­ного поля в часі в якій-небудь точці поля порушує вихор або ротор електричного поля в тій же точці поля, тобто визи­ває вихрове електричне поле.

Друге рівняння Максвелла є диференціаль­ною формою закону електромагнітної індукції.

Щоб переконатися в цьому, проведемо наступні міркування. У думках візьмемо деякий замкнутий контур, розташований в змінному електромагніт­ному полі. Змінний магнітний потік, що проходить через контур, наведе в ньому ерс. . Але, тому 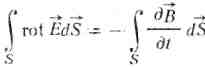, причому площа S спирається на контур l.

На підставі теореми Стоксу тому:

(22.5)

Рівність (22.5) повинна виконуватися при будь-яких площах S, що можливо тільки у тому випадку, коли рівні підінтегральні функції обох інтегралів. Отже:

Знак «мінус» в правій частині другого рівняння Максвелла (як і у формулі пояснюється тим, що в основу покладено правило правого гвинта. Якщо загвинчувати правий гвинт так, що позитивний напрям вектора магніт­ної індукції в деякій точці простору при зростанні індукції в цій точці збігається з напрямом руху вістря гвинта, то позитивне на­правлення для вектора напруженості електричного поля при складанні циркуляції вектора уподовж нескінченно малого контура, що оточує цю точ­ку і лежачого в площині, перпендикулярній вектору , збігається з напрямом обертання головки гвинта.

Знак «мінус» в правій частині (22.4) поставлений для того, щоб привести в відповідності дійсний напрям за обумовлених раніше умов з напрямом, прийнятим для за позитивне.

Як у першому, так і в другому рівняннях Максвелла беруть участь частинні (не повні) похідні в часі. Пояснюється це тим, що рівняння Максвелла записані для таких тіл і контурів, які нерухомі по відношенню до вибраної системи координат.

У змінному електромагнітному полі окрім силових ліній елек­тричного поля, що «починаються» і «закінчуються» на електричних зарядах (як в електростатичному полі) можуть бути і замкнуті на себе силові лінії електричного поля, що охоплюють замкнуті на себе силові лінії магнітного поля .

Рівняння Максвелла в комплексній формі запису. Рівняння (22.1) і (22.4) записані для миттєвих значень. Якщо Н і Е змінюються в часі синусоїдально, то можна скористатися сим­волічним методом і записати рівняння (22.1) і (22.4) в іншій формі. Нехай і

Можна записати (I_т — уявна частина) або, умовно, , де комплексна амплітуда

У свою чергу ( знак відповідності).

Оскільки напруженості Е і І, крім того, що вони міняються в часі по синусоїдальному закону, є функціями векторни­ми, тобто певним чином орієнтованими в просторі век­торами, то над ними ставлять стрілку і крапку: і

Стрілка означає, що мова йде про вектор в просторі, крапка — про те, що проекції цього вектора на будь-яку з координатних осей в часі змінюються синусоїдально.

Тоді можна замінити на

і

як постійну величину, не залежну від координат, можна винести за знак ротора). При цьому перше рівняння Максвелла запи­шем так:

Після скорочення на отримаємо:

(22.6)

Аналогічно, друге рівняння Максвелла в комплексній формі:

(22.7)