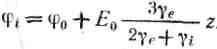17.Аналогії між полем в провідному середовищі і електростатичним полем. Співвідношення між провідністю і ємністю.

За своєю природою поле електростатичне і поле по­стійного струму в провідному середовищі різні. Електростатичне поле створюється електричними зарядами, незмінними в часі і нерухомими в просторі, тоді як електричне поле в прові­дному середовищі — це поле, в якому електричні заряди мають впорядкований рух під дією зовнішнього джерела. Тим не менше між двома полями можна провести певну формальну аналогію.

Дійсно, електростатичне поле в областях, не зайнятих зарядами, задовольняє рівнянню Лапласа. Електричне поле по­стійного струму в провідному середовищі поза сторонніми джерелами також йому задовольняє. У обох полях мають справу з вектором напруженості поля . З вектором електричного зсуву можна зіставити вектор щільності струму . З потоком вектора (позначимо його буквою можна підставити потік векто­ра щільності електричного струму .

Граничні умови на поверхні розділу двох діелектриків:

Граничні умови на поверхні розділу двох середовищ з різною провідністю:

Але якщо два поля задовольняють одному і тому ж рівнянню і в них виконуються тотожні граничні умови для схожих величин, то при однаковій формі граничних поверхонь на підставі теореми єдності можна сказати, що сукупність силових і еквіпотенціальних ліній в цих двох полях (тобто картина поля) буде однаковою.

Ця формальна аналогія широко використовується на практиці. Так, наприклад, якщо яке-небудь електростатичне поле вже вивчене, то всі відомості про нього можуть бути перенесені і на геометрично подібне поле в провідному середовищі. Справедливо і зворотне заклю­чення.

Співвідношення між провідністю і ємністю. Якщо які-небудь електроди помістити в провідне середовище і приєднати до джерела ерс., то в провідному середовищі піде струм. Якщо напруга між електродами 1 і 2 рівно і по середовищу проходить струм І,то про­відність між електродами 1 і 2

Оскільки струм ,

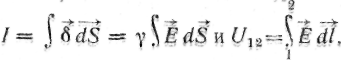то 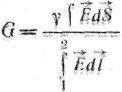^(17.1)

У свою чергу, в електричному полі з електродами таких же параметрів ємність між двома частинами електродів, на яких розміщені однакові по величині і протилежні по знаку за­ряди Q, що створюють потік  вектора електричної індукції , буде

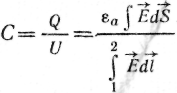^(17.2)

Якщо розділити (17.2) на (17.1), то після скорочення отримаємо

, (17.3)

тобто ємність С між двома тілами, розділеними діелектриком з абсолютною діелектричною проникністю , так відноситься до про­відності G між тими ж тілами, якщо помістити їх в середовище з елек­тричною провідністю , як відноситься до .

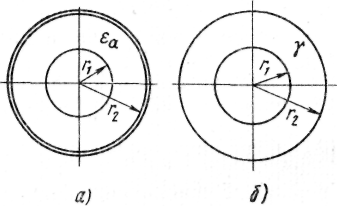
Рисунок. 17.1

Співвідношення (17.3) дозволяє по відомому виразу ємності між якими-небудь тілами отримати вираз для провідності або зробити зворотну опера­цію. Так, наприклад, ємність двопровідної лінії:

(17.4)

де l — довжина проводів;

d — відстань між осями про­водів;

r — радіус дроту.

Ємність коаксіального кабелю (рис. 17.1, а) розраховується:

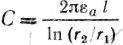
Провідність між двома співвісними циліндрами довжиною l, ко­трі розділені середовищем з провідністю (рис. 17.1, б)

Аналогію можна розповсюдити і на складніші поля. На­приклад, якщо в рівномірне поле, створене в середовищі з провідністю, помістити кулю з провідністю, то відповідно по­тенціал усередині кулі визначимо таким чином: