1. Використання законів Кірхгофа для розрахунку електричних кіл.

Закони Кірхгофа.

Всі електричні кола підкоряються першому і другому законам (правилам) Кірхгофа.

Перший закон Кірхгофа можна сформулювати двояко:

1. алгебраїчна сума струмів, що входять до будь-якого вузла схеми, дорівнює нулю;

2. сума струмів, що входять до будь-якого вузла, дорівнює сумі струмів що виходять з вузла.

Якщо струми, що входять у вузол, вважати за додатні, а що виходять — від’ємні, то згідно першому формулюванню:

(1.1.)

згідно другому:

(1.2.)

Фізично перший закон Кірхгофа означає, що рух за­рядів в ланцюзі відбувається так, що ні в одному з вузлів вони не накопичуються.

Якщо уявно розітнути будь-яку схему довільною площиною і все що знаходиться по одну сторону від неї розглядати як деякий великий "вузол", то алгебраїчна сума струмів, що входять в цей "вузол", дорівнюватиме нулю.

Другий закон Кірхгофа також можна сформулювати двояко:

1) алгебраїчна сума падінь напруги в будь-якому замкнутому контурі дорівнює алгебраїчній сумі ЕРС уздовж того ж кон­тура:

(1.3.)

(у кожну з сум відповідні доданки входять із знаком плюс, якщо вони збігаються з напрямом обходу контура, і із знаком мінус, якщо вони не збігаються з ним);

2) алгебраїчна сума напруги уздовж будь-якого замкнутого контура дорівнює нулю:

(1.4)

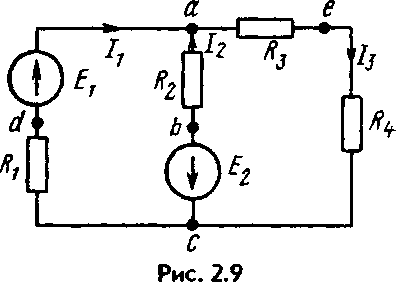
Для периферійного контура схеми рис. 2.9:

(1.5.)

Закони Кірхгофа справедливі для лінійних і нелінійних кіл при будь-якому характері зміни в часі струмів і напруг.

Зробимо два зауваження:

1) запис рівняння по другому закону Кирхгофа у формі (1.3) може бути отриманий, якщо обійти який-небудь контур деякої схеми і записати вираз для потенціалу довільної точки цього контура через потенціал цієї ж точки (узявши її за початкову при обході) і спад напруги та ЕРС;

2) при записі рівнянь по другому закону Кірхгофа у формі (1.4) напруга U_ki ділянок кола включає і спад напруги ділянок, і присутні на цих ділянках ЕРС.

Складання рівнянь для розрахунку струмів в схемах з допомогою законів Кірхгофа.

Закони Кірхгофа використовують для зна­ходження струмів у вітках схеми. Позначимо число всіх віток схеми В, число віток, що містять джерела струму, — В_джс і число вузлів У. У кожній гілці схеми тече свій струм. Оскільки струми в вітках з джерелами струму відомі, то число невідомих струмів дорівнює В-В_джс. Перш ніж скласти рівняння, необхідно довільно вибрати:

а) додатні напрями струмів в вітках і позначити їх на схемі;

б) додатні напрями обходу контурів для складання рівнянь по другому закону Кірхгофа.

З метою одноманітності рекомендується, для всіх контурів додатній напрям обходу вибирати однаковими, наприклад за годинниковою стрілкою.

Щоб отримати лінійно незалежні рівняння, по першому закону Кірхгофа складають рівняння, число яких рівне на одиницю менше чис­ла вузлів, тобто У-1.

По другому закону Кірхгофа складають рівняння, число яких дорівнює числу віток без джерел струму (В-В_джс), з врахуванням рівнянь, складених по першому закону Кірхгофа, тобто: (В-В_джс)-(У—1) = В-В_джс-У+1.

Складаючи рівняння по другому закону Кірхгофа, потрібно використати всі вітки схеми, виключаючи лише гілки з джерелами струму.

Якщо спробувати скласти рівняння по другому закону Кірхгофа у формі (1.3) для контура, в який входить джерело струму, то в нього увійшли б нескінченно великі доданки і воно не мало б сенсу.

При записі лінійно незалежних рівнянь по другому закону Кірхгофа прагнуть, щоб в кожен новий контур, для якого складають рівняння, входила хоч би одна нова вітка, яка не входила в попередні контури, для яких вже записані рівняння по другому закону Кірхгофа. Такі контури називаються незалежними.

Умова, щоб в кожен новий контур входила хоч би одна нова вітка, є достатньою, але не необхідною умовою, а тому її не завжди виконують. У таких випадках частину рівнянь по другому закону Кірхгофа складають для контурів, всі вітки яких вже увійшли до попередніх контурів.