2. Нормальні напруження при чистому згині. Визначимо величину нормальних напружень, що виникають при чистому згині бруса.

Якщо до двохопорної балки прикласти однакові пари сил М (рис.7.9,а), то в довільних перерізах такої балки Q=0, а M=const.

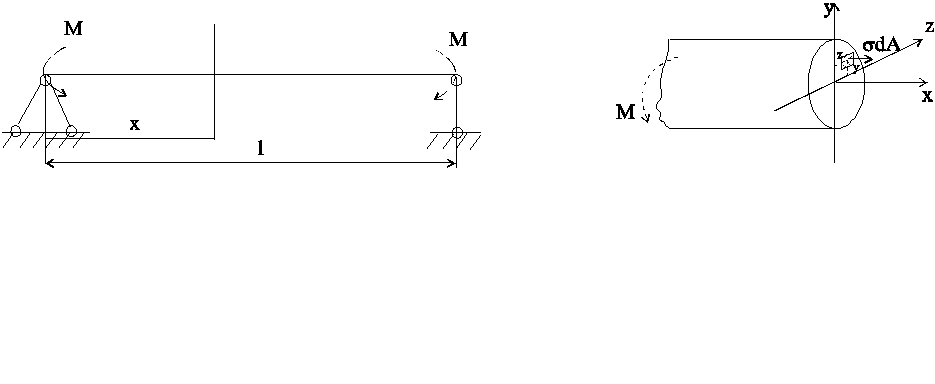
а) Рис.7.9 б)

Виділимо в поперечному перерізі балки х елементарну площадку dA, на яку діє нормальне зусилля σdA (рис.7.9,б), тобто розглянемо статичну сторону задачі. Із шести рівнянь рівноваги залишається тільки три:

. (1)

Останнє рівняння дає інтегральний зв‘язок між нормальним напруженням  у перерізі балки і прикладеним до неї моментом.

Розглядаючи геометричний бік задачі, одержимо

, (2)

де y – координата точки перерізу,  - кривизна нейтральної лінії,  - лінійна деформація.

Закон Гука буде виражати фізичний бік задачі

. (3)

Сумісно розв‘язуючи систему рівнянь (1), (2) і (3) матимемо:

(закон Гука при згині); (4)

(нормальне напруження при чистому згині).

Тут – жорсткість при згині.

Екстремальні нормальні напруження при згині балки виникають у крайніх точках її перерізу, найбільш віддалених від нейтральної осі:

. (5)

Величина (осьовий момент опору перерізу балки). Тоді

. (6)

При чистому згині підтверджується гіпотеза плоских перерізів, і тому одержані результати (6) є точними з точки зору теорії пружності.

3

Рис.7.10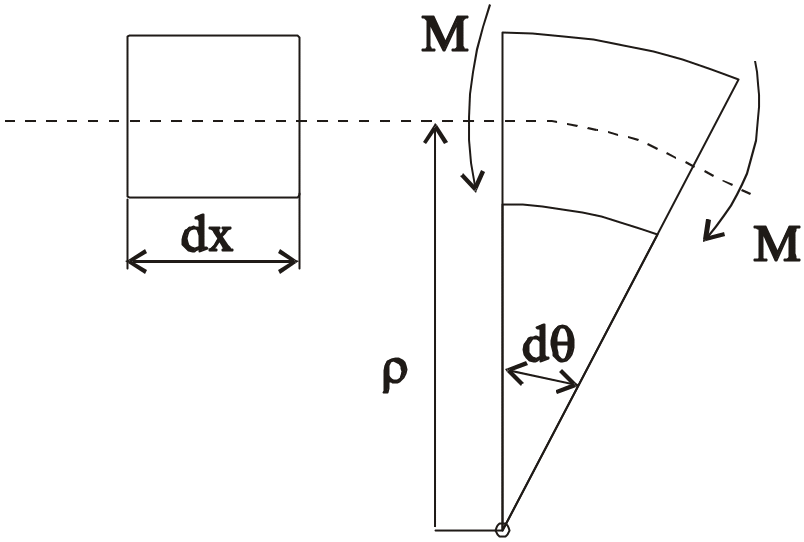

. Потенціальна енергія при згині. Визначимо потенціальну енергію при чистому згині.

Розглянемо ділянку бруса dx (рис.7.10). Потенціальна енергія згину дорівнює роботі моменту М на взаємному кутовому переміщенні d:

,

причому , де  – радіус кривизни нейтрального шару розглядуваної ділянки бруса. На основі закону Гука при згині . Підставляючи значення d, матимемо

.

Для всього бруса завдовжки l

. (7)

4. Згин пружнов’язкої балки. Розглянемо розрахунковий випадок чистого згину. Вісь бруса позначимо через х, згинаючі моменти на кінцях – М. При розгляді чистого згину знову використовується гіпотеза плоских поперечних перерізів, як і при розгляді простого розтягу.

Нехай ε_х=ε, σ_х=σ. Тоді для відносного подовження волокна можна записати таку формулу:

, (8)

де В – кривизна осі балки в перерізі, що розглядається; у-відстань волокна від нейтрального шару.

Відповідно для будемо мати

. (9)

Тут використовуємо вже відому залежність між деформацією і часом для кривої повзучості, яка має вигляд

. (10)

Підставляючи в (10) вирази (8) і (9) і перемножуючи кожну складову на у, отримаємо

.

Проінтегруємо ліву і праву частини цієї рівності по всій площі перерізу. Тоді будемо мати

.

Позначимо: ; , де М – згинаючий момент в перерізі, І – осьовий момент перерізу відносно нейтральної осі.

Враховуючи, що , останнє рівняння запишемо так:

. (11)

Вважаючи, що прогини балки малі в порівнянні з її довжиною, можна прийняти

. (12)

Враховуючи залежність (12), рівність (11)запишемо у вигляді

, (13)

де . (14)

Якщо М=М₀=const, то і рівняння (13) приймає вигляд

. (15)

При сталому навантаженні, тобто при М₀=const, розв’язок рівняння (15) запишемо так:

.

Слід зазначити, що вираз для напруження в будь-якій точці поперечного перерізу балки в даному випадку залишається сталим і рівним , тобто в’язкість впливає лише на кривизну балки. У випадку статично невизначуваної балки цей висновок не відповідає дійсності. Якщо в будь-який момент часу t₂ відпустити на кінцях балки прикладені згинаючі моменти, то зміна кривизни буде відбуватися згідно закону

,

де - кривизна балки при t=t₂.

Графік зміни в часі кривизни балки в цьому випадку показано на рис.7.11.

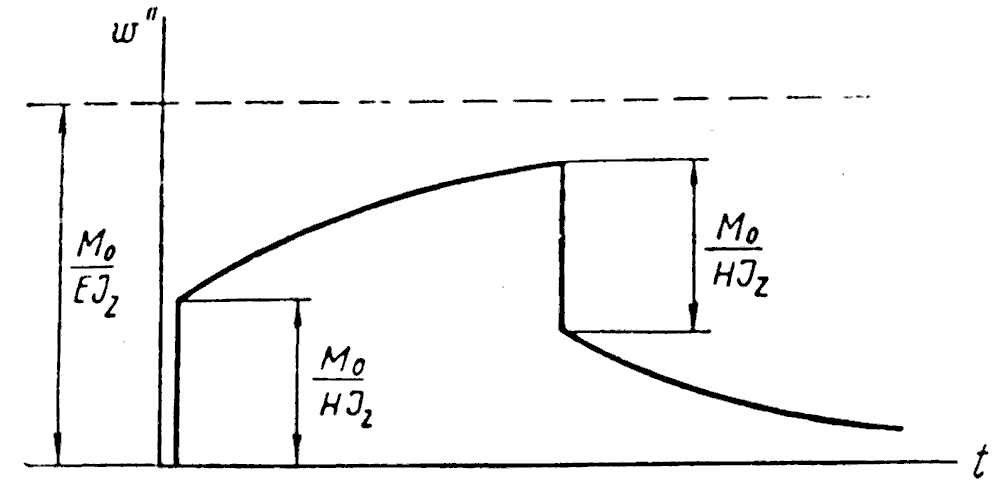
Рис.7.11

Лекція 13. Поперечний згин. Нормальні напруження. Розрахунок на міцність при згині. Раціональна форма поперечного перерізу балки.

1. Поперечний згин. Нормальне напруження. При поперечному згині у поперечних перерізах балки, крім згинаючих моментів, виникають ще й поперечні сили і зв‘язані з ними дотичні напруження. При дії дотичних напружень з‘являється деформація зсуву і поперечні перерізи балки скривлюються. Внаслідок цього гіпотеза плоских перерізів не відповідає дійсним деформаціям, і для визначення нормальних напружень у балці треба в кожному конкретному випадку розв‘язувати складну задачу теорії пружності. Різниця між напруженнями, обчисленими за формулою для чистого згину і за формулами для напружень при поперечному згині, одержаними методами теорії пружності, є тим меншою, чим більше відношення довжини прольоту l до висоти перерізу h.

Наприклад, при згині рівномірно розподіленим навантаженням простої балки прямокутного перерізу різниця ця для відношення дорівнює 1,7%, а для відношення – 6,7%. При розрахунках на поперечний згин балок з відношенням довжини прольоту l до висоти перерізу h порядку нормальні напруження визначають за формулою

,

де I_z – момент інерції відносно нейтральної осі перерізу. Для балки з поперечним перерізом, симетричним відносно нейтральної осі, максимальне нормальне напруження у небезпечному перерізі дорівнює

. (1)

При розрахунках балок з відношенням треба користуватися тільки точними формулами теорії пружності.

2. Розрахунок на міцність при згині. Ми розглянули нормальні напруження, що виникають при чистому та поперечному згині балки. Далі ми розглянемо дотичні напруження, які виникають лише при поперечному згині. Виявляється, що у переважній більшості випадків дотичні напруження грають другорядну роль, і міцність балки залежить, в першу чергу, від величини максимальних нормальних напружень, що виникають у її небезпечному перерізі.

При розрахунках на міцність методом допустимих напружень вважають, що міцність балки буде забезпечена, коли задовольняється умова .

Підставляючи _max за формулою (1), одержимо умову міцності балки з перерізом, симетричним відносно нейтральної осі:

. (2)

З цієї умови випливає формула для підбору поперечного перерізу такої балки

. (3)

За одержаним значенням осьового моменту опору підбираємо відповідний стандартний профіль.

Для перерізів, несиметричних відносно нейтральної осі, за формулою (3) визначається менший з двох моментів опору перерізу. У випадку балок, виготовлених з матеріалів, що неоднаково працюють на розтяг і стиск, перевірку міцності треба вести окремо для розтягнутих і стиснутих волокон.

3. Раціональна форма поперечного перерізу балки. З підбором поперечного перерізу балки зв‘язане питання його раціональної форми. Оскільки основний вплив на міцність балки при згині мають нормальні напруження, які збільшуються із зростанням віддалі від нейтральної осі, найбільш раціональними є такі перерізи, в яких як можна більше матеріалу розташовано далеко від нейтральної осі. Прикладами таких перерізів є перерізи типу двотавра.

Для балок, матеріал яких неоднаково працює на розтяг і стиск, раціональними несиметричними перерізами є такі, у яких віддалі крайніх точок від нейтральної осі пропорціональні величині допустимих напружень для розтягу і стиску.

Лекція 14. Дотичні напруження при згині. Загальна схема розв‘язання задач про визначення дотичних напружень у пружному тілі. Формула Журавського для визначення дотичних напружень. Поняття про центр згину.

1. Дотичні напруження при згині. При поперечному згині бруса в його перерізах, крім згинального моменту, діє поперечна сила, що намагається зсунути переріз один відносно одного. У цьому випадку, крім нормальних напружень від згинального моменту, у перерізах бруса виникають дотичні напруження. На основі закону парності дотичних напружень останні виникають і в поздовжніх перерізах бруса. Виникнення дотичних напружень супроводжується появою кутових деформацій зсуву. Внаслідок цього поперечні перерізи бруса при згині його не залишаються плоскими. Однак, як показали теоретичні та експериментальні дослідження поперечного згину, викривлення поперечних перерізів істотно не впливають на величину нормальних напружень. Тому при поперечному згині користуються формулами, одержаними для чистого згину.

2. Загальна схема розв‘язання задач про визначення дотичних напружень у пружному тілі. У загальному випадку поперечного згину балки довільного перерізу дотичні напруження визначають, виходячи із загальних рівнянь рівноваги і переміщень, методами теорії пружності, що зв’язане із значними математичними труднощами.

У курсі опору матеріалів при виведенні формул для дослідження напруженого стану бруса будемо дотримуватися такої схеми.

а) Розглядаємо статичний бік задачі, тобто записуємо ті рівняння, які потрібні для задачі.

б) Розглядаємо геометричний бік задачі: на базі експериментального вивчення даного виду деформації стержня та певних гіпотез установлюємо залежності між переміщеннями точок стержня та їхнім положенням у перерізі відносно вибраної системи координат. Ці залежності називаються геометричними рівняннями.

в) Розглядаємо фізичний бік задачі: на підставі експериментальних досліджень фізичних властивостей матеріалу визначаємо залежність між напруженнями та деформаціями (фізичні рівняння).

г) Виконуємо синтез, тобто розв‘язуємо всі рівняння.

Отже, задача про обчислення напружень у перерізі завжди є статично невизначуваною і потребує розгляду трьох аспектів. Проте можна прийняти такі гіпотези про розподіл напружень, при яких задача стане статично визначуваною. Тоді немає потреби використовувати геометричні та фізичні рівняння. Саме так була виведена формула для визначення t при поперечному згині. Формулу для обчислень t вивів Журавський на прикладі балки прямокутного перерізу.