3. Диференціальні залежності між m, q і q. Установимо залежність між інтенсивністю розподіленого навантаження, поперечною силою і згинаючим моментом.

Розглянемо балку, навантажену розподіленим навантаженням інтенсивності q(x) (рис.7.4,а).

а) Рис.7.4 б)

Двома безмежно близькими поперечними перерізами виділимо з балки елемент довжиною dx (рис.7.4,б). Як згинаючі моменти, так і поперечні сили можуть змінюватися при переході від одного перерізу x до другого x+ dx.

Під дією прикладеного навантаження виділений елемент (рис.7.4,б) перебуває у рівновазі. З умов рівноваги елемента одержимо:

. (1)

Продиференціюємо останній вираз по змінній x: . (2)

Як видно з одержаних диференціальних рівнянь, функції M(x), Q(x) і q(x) зв‘язані між собою, і вид однієї з них обумовлює вид двох інших. Ці залежності доцільно використовувати при перевірці правильності побудови епюр M(x) і Q(x).

Розглянемо випадок, коли на балку діють одночасно довільне вертикальне q(x) і моментне m(x) навантаження. На рис.7.4 моментне навантаження m(x) не показане.

Враховуючи m(x), будемо мати такі вирази:

,

,

де Q^*(x) – узагальнена поперечна сила.

Тут .

Тоді ,

де q^*(x) – інтенсивність узагальненого навантаження;

.

Якщо m(x)=0 або m(x)=const, то q^*(x)=q(x).

Якщо q(x)=0, то .

Запишемо, що Q^*(x) – перша похідна від М(х). Взагалі між М(х), Q^*(x) і q^*(x) існують диференціальні і інтегральні залежності.

4. Епюри згинаючих моментів і поперечних сил. Розглянемо побудову епюр згинаючих моментів і поперечних сил для балок з різним навантаженням.

Нехай консольна балка закріплена одним кінцем жорстко, а на другому кінці прикладена зосереджена сила Р (рис.7.5). Для консольних балок завжди будемо брати вільний кінець за початок координат.

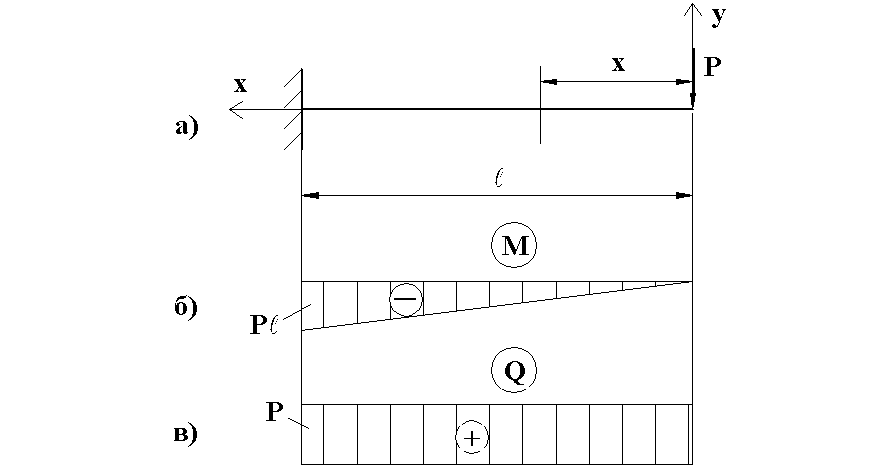
Рис.7.5

В даному разі маємо одну ділянку. Для ділянки 0≤х≤ℓ маємо

,

.

Значення згинаючого моменту

М(0)=0, М(ℓ)= -Р∙ℓ.

Поперечна сила всюди стала і дорівнює Р.

Епюри М і Q побудовані на рис.7.5,б і в.

Розглянемо балку на двох опорах, навантажену зосередженою силою Р (рис.7.6,а). Спочатку з умов рівноваги визначимо опорні реакції

:

,

;

:

,

.

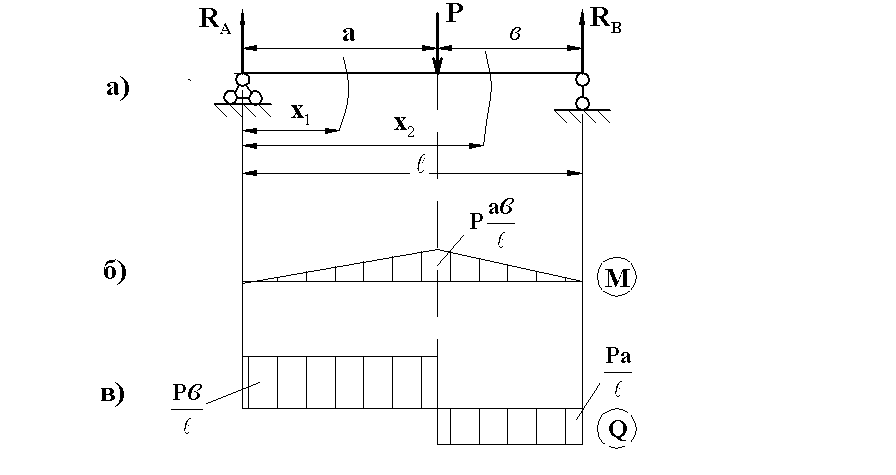
Рис. 7.6

Сила Р розділяє прольот балки на дві ділянки. Для лівої ділянки при 0≤х₁≤а маємо

,

.

Значення згинаючого моменту у характерних точках

М(0)=0, .

Для правої ділянки при а≤х₂≤ℓ

,

.

Для характерних точок маємо

, М(ℓ)=0.

За одержаними значеннями Q і М побудовані їх епюри на рис.7.5 б,в. Тут згинаючі моменти змінюються за законами прямої лінії, а поперечні сили є сталими і на відповідних ділянках відрізняються тільки знаком. Ординати епюр Q і М відкладаються від нульових ліній.

Далі розглянемо навантаження інтенсивності q, рівномірно розподілене по довжині прольоту балки (рис.7.7)

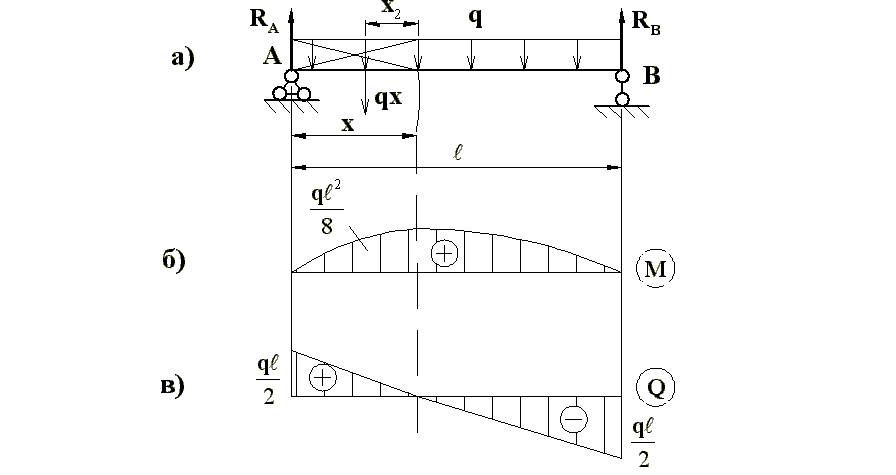
Рис.7.7

Внаслідок симетрії реакції опор будуть рівні між собою .

Для 0≤х≤ℓ обчислимо згинаючий момент і поперечну силу

,

.

Отже, згинаючий момент змінюється за законом квадратної параболи. Поперечна сила змінюється по довжині балки за законом прямої лінії. Характерні значення поперечної сили

, .

Для визначення екстремального значення монету знаходимо похідну від М(х) по абсцисі х перерізу

.

У перерізі , в якому Q=0, згинаючий момент має максимальне значення

.

Епюри М і Q побудовані на рис.7.7 б,в.

Далі запишемо перший і другий інтеграли диференційного рівняння:

.

Графічне зображення першого і другого інтегралів дають епюри для поперечних сил (рис.7.7,в) і згинаючих моментів (рис.7.7,б).

Для розглядуваної балки (рис.7.7,а) маємо: m(x)=0, тоді q^*(x)=-q(x)=-q, Q^*(х)= Q(х), а диференціальне рівняння має вигляд

.

Перший інтеграл .

Другий інтеграл . Для знаходження довільних сталих будемо мати дві граничні умови: при х=0 і при х=ℓ момент М=0. Враховуючи граничні умови, знаходимо ; .

Тоді ;

.

Розглянемо навантаження інтенсивності q, рівномірно розподілене по всій довжині консолі (рис.7.8). Тут маємо одну ділянку, абсциса перерізу змінюється: 0≤х≤ℓ, тобто приймаємо початок осі х на вільному кінці консолі.

Тоді для згинаючого моменту і поперечної сили будемо мати

, .

В даному випадку епюра М(х) буде квадратною параболою, дотичною до осі х в кінці консолі, а Q(x) – прямою. Характерні значення М(х) і Q(x):

, ;

, .

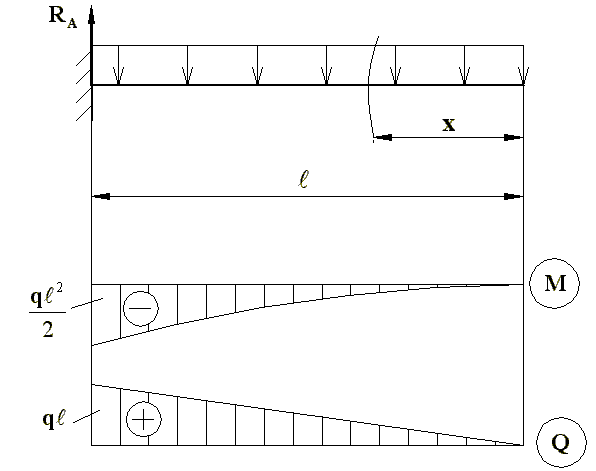
Рис.7.8

Епюри М і Q наведено на рис.7.8. Знаки М і Q всюди на епюрах не мають фізичного смислу, тому в розрахунках момент і поперечні сили беруть за абсолютними значеннями.

Лекція 12. Чистий згин. Нормальні напруження при чистому згині. Потенціальна енергія при згині. Згин пружнов’язкої балки.

4. Чистий згин. При відсутності поперечних сил і наявності одних лише згинаючих моментів в перерізах згин називається чистим (Q=0, M=const).

В основу елементарної теорії згину покладені такі припущення:

а) при чистому згині первісно плоскі перерізи бруса не викривляються, залишаються плоскими і при деформації обертаються один відносно другого (гіпотеза плоских перерізів);

б) поздовжні волокна бруса зазнають простого розтягу або стиску, не спричинюючи взаємного бокового тиску.

По висоті перерізу бруса деформація розтягу і стиску змінюється безперервно. Отже, можна припустити наявність всередині бруса (симетричний переріз) шару, що відділяє зону розтягу від зони стиску. Волокна, розміщені в цьому шарі, не зазнають ніякої деформації. Такий шар називається нейтральним. Лінія перетину нейтрального шару з площиною поперечного перерізу бруса називається нейтральною.