Розв’язання задач по темі “Кручення”

Задача 6.1. Вал передає момент М=10000 Н∙м. Треба підібрати розміри поперечного перерізу вала для двох розрахункових випадків: а) для суцільного кругового перерізу; б)для кругового перерізу із отвором (d=7D/8). Порівняти обидва перерізи за витратою матеріалу. Допустиме напруження [τ]=60 МПа.

Розв’язання. За формулою для обох перерізів см³.

Для суцільного перерізу згідно виразу маємо

см³ ; D=9,43 см.

Для трубчастого перерізу згідно виразу маємо

см³;

D=12,6 см.

Витрата металу пропорціональна площі поперечного перерізу

см²,

для другого випадку

см².

Таким чином, трубчастий переріз є більш економічний і в даному випадку (при ) витрата металу зменшується більше, чим в 2 рази.

Слід зазначити, що для перерізу з отвором напруження розподілені більш рівномірно і використання матеріалу стає значно ефективнішим.

Задача 6.2. Трубчастий стальний вал завдовжки ℓ=1,2 м передає потужність N=200 квт при кутовій швидкості ω=20 рад/с. Визначити внутрішній d та зовнішній D діаметри вала та його кут закручування φ, якщо допустимі напруження [τ]=60 МПа, а відношення діаметрів має бути ; G=8∙10⁴ МПа=8∙10³ кН/см².

Розв’язання. За формулою кн∙м=1000 кн∙см.

З умови міцності

см.

Отже, d=0,8D=9,1 см.

Знаходимо полярний момент інерції перерізу вала:

см⁴.

Кут закручування вала знаходимо згідно виразу

рад.

Задача 6.3. На стальному валі є один ведучий і три ведені шківи (рис.6.6). Віддаль а=0,5 м. Потужності на шківах дорівнюють N₁=16 квт, N₂=32 квт, N₃=8 квт при n=100 обертів вала за 1 хв. Шківи на рисунку не показані.

Треба побудувати епюру крутячих моментів; підібрати діаметр вала сталого поперечного перерізу з умови міцності при [τ]=100 МПа і з умови жорсткості при допустимому куті закручування на 1 м довжини вала [θ]=2°/м; побудувати епюру кутів закручування, відраховуючи кути від перерізу ведучого шківа. Прийняти для сталі G=8∙10⁴ МПа.

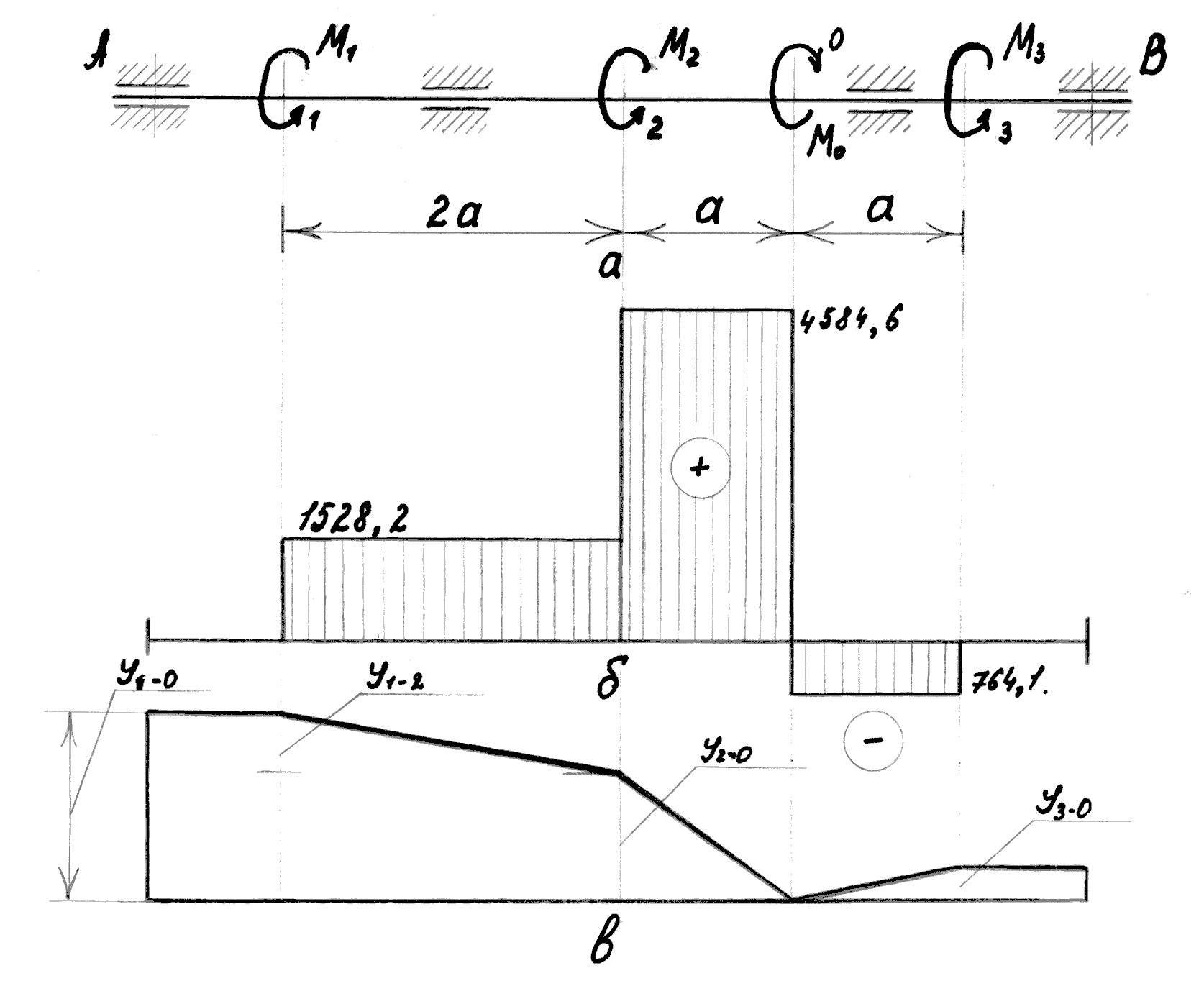
Рис. 6.6

Розв’язання. Потужність N₀ на ведучому шківі дорівнює сумі потужностей на ведених шківах, тобто

кВт.

Величини моментів, які передаються на вал від окремих шківів, можна визначити за формулою

[нм].

Тоді нм; М₂=2М₁=3056,4 нм; М₃=0,5∙М₁=764,1 нм.

Момент М₀ на ведучому шківі дорівнює сумі моментів на ведених шківах:

нм.

Величина крутячих моментів на окремих ділянках вала дорівнює:

на ділянці А-1

М_К=0;

на ділянці 1-2

М_К=М₁=1528,2 нм;

на ділянці 2-0

М_К=М₁+ М₂=1528,2+3056,4=4584,6 нм;

на ділянці 0-3

М_К=-М₃=-764,1 нм.

За одержаними даними на рис.6.6,б побудована епюра крутячих моментів. Максимальний крутячий момент дорівнює М_К=4584,6 нм.

Діаметр вала, обчислений з умови міцності, дорівнює

м.

Діаметр вала, обчислений з умови жорсткості, дорівнює

м.

Отже, діаметр вала вибираємо з умови жорсткості d=70 мм.

Кути закручування на окремих ділянках вала обчислюємо за формулою . Визначаємо величину полярного моменту інерції поперечного перерізу вала

м⁴.

Кут повороту перерізу А відносно перерізу 1 дорівнює нулеві. Кут повороту перерізу 1 відносно перерізу 2

.

Кут повороту перерізу 2 відносно перерізу 0

.

Кут повороту перерізу 1 відносно перерізу 0 дорівнює сумі кутів φ_1-2 і φ_2-0:

φ_1-0=0,46°+0,70°=1,16°.

Кут повороту перерізу 3 відносно перерізу 0

.

Кут повороту перерізу В відносно перерізу 3 дорівнює нулеві. Епюра кутів закручування побудована на рис.6.6,в

Максимальний відносний кут закручування на 1м довжини вала виникає на ділянці 2-0 і дорівнює .

Задача 6.4. Ступінчастий стальний брус, затиснутий обома кінцями, скручується моментом М=200 н·м (рис.6.7,а). Побудувати епюри крутячих моментів і кутів повороту. Визначити потенціальну енергію кручення круглого бруса. Модуль зсуву G=8·10⁴ МПа.

Розв’язання. Задана система є один раз статично невизначувана. Розкриваємо статичну невизначуваність. Для цього відкинемо ліве закріплення і його дію на брус (вал) замінимо моментом М_А (рис.6.7,б). Цей момент визначимо з умови: поворот лівого кінця бруса відносно правого дорівнює нулю. Кут повороту перерізу А α_А може бути визначений як алгебраїчна сума кутів повороту α_А1, викликаного дією моменту М_А,, і α_А2, викликаного дією моменту М. Отже, α_А=α_А1+ α_А2=0.

Від дії моменту М_А в поперечних перерізах всіх трьох (І, ІІ, ІІІ) ділянок бруса виникає однаковий крутячий момент .

Тоді .

Полярні моменти інерції поперечних перерізів окремих ділянок бруса дорівнюють

см⁴,

см⁴.

Отже, рад.

Від дії момента М крутячі моменти на окремих ділянках бруса (рис.6.7,б)

Н∙м.

Тоді маємо

рад.

Підставимо значення α_А1 і α_А2 у вираз для α_А:

,

звідки Н∙м.

Остаточно крутячі моменти, які діють в поперечних перерізах бруса, дорівнюють сумі моментів від дії моментів М_А і М:

Н∙м;

Н∙м;

Н∙м.

Епюру крутячих моментів показано на рис.6.7,в. Визначаємо кути закручування на окремих ділянках бруса:

рад;

рад;

рад.

Остаточно знаходимо кути повороту перерізів:

рад;

рад;

.

Нульове значення кута повороту α_В свідчить про вірне визначення крутячих моментів. Епюра кутів повороту побудована на рис.6.7,г.

Потенціальну енергію деформації кручення, яка накопичується в брусі, знаходимо за формулою

=0,538 дж.

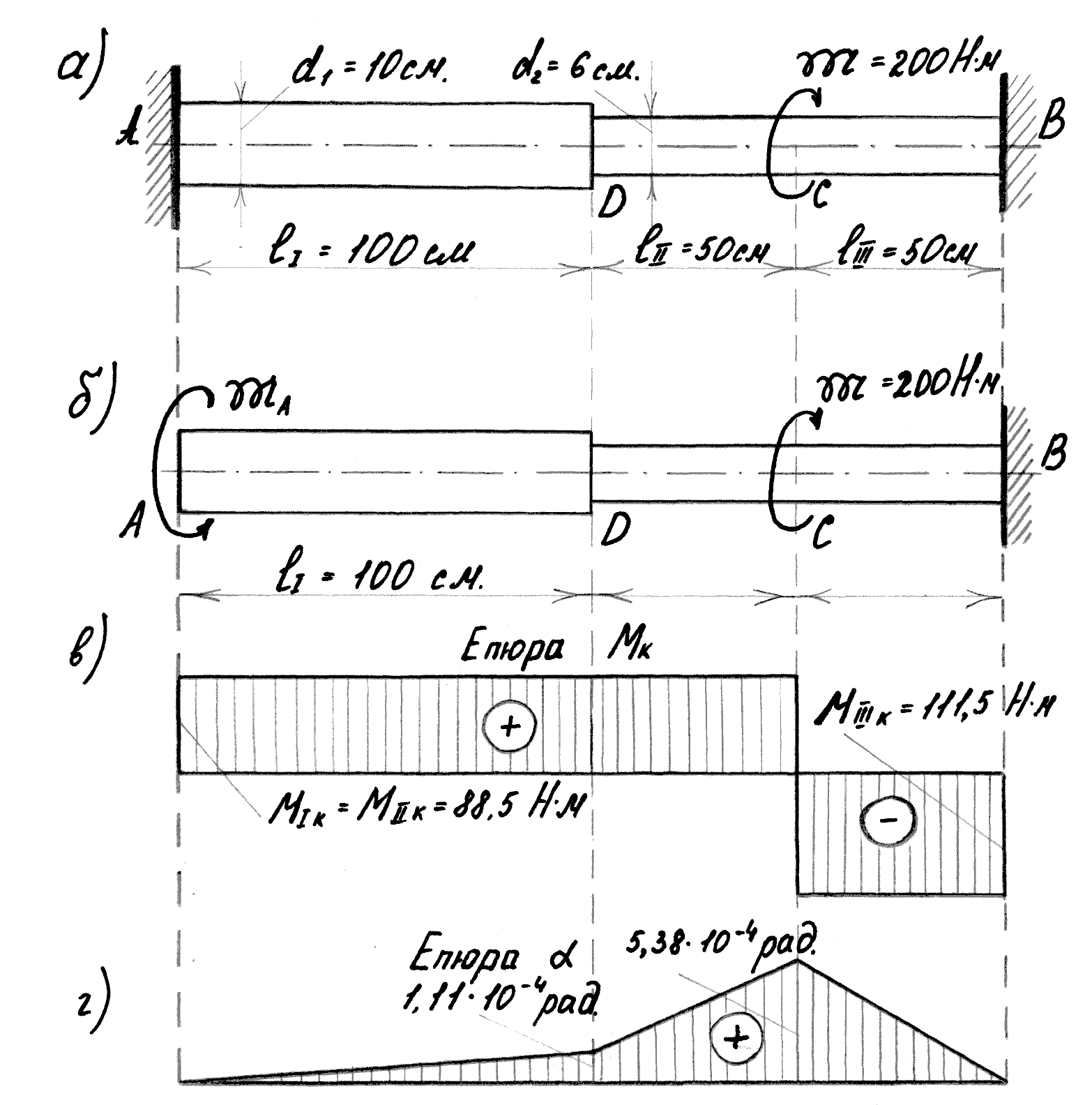
Рис.6.7

Задача 6.5. Для заданої системи пружин (рис.6.8,а) треба визначити максимальні дотичні напруження в усіх пружинах і переміщення точки А, якщо діаметри витків пружин D₁=16 см, D₂=8 см, D₃=10 см; діаметри стержнів пружин d₁=3 см, d₂=1 см, d₃=2 см; кількість витків пружин n₁=10, n₂=30, n₃=20. Матеріал – сталь має модуль зсуву G=8∙10⁴ МПа, Р=1 кН.

Розв’язання. Х₁, Х₂, Х₃ – реакції, що виникають в опорних витках пружин (рис.6.8,б).

З рівняння рівноваги випливає, що

.

Отже, задача двічі статично невизначувана. Треба скласти два додаткових рівняння переміщень на тій основі, що подовження ∙λ₁ і λ₂ верхніх пружин рівні між собою і рівні скороченню λ₃ нижньої пружини:

λ₁₌λ₂₌λ_3. (а)

Використовуючи формулу , запишемо ці умови так:

; (б)

. (в)

Розв’язуючи систему рівнянь (а), (б) і (в), знайдемо

; .

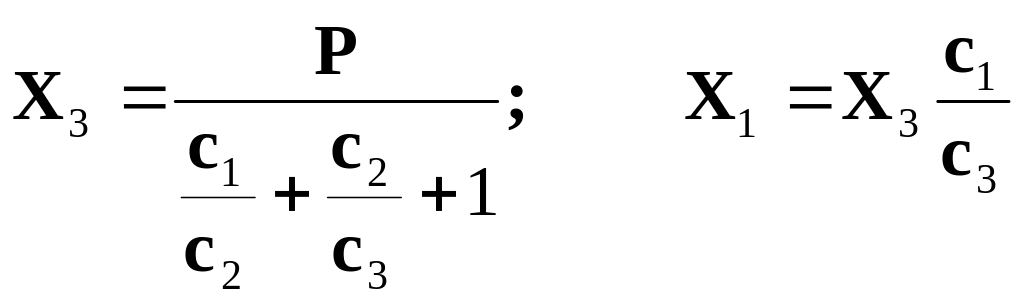Визначимо відношення жорсткостей пружин

;

.

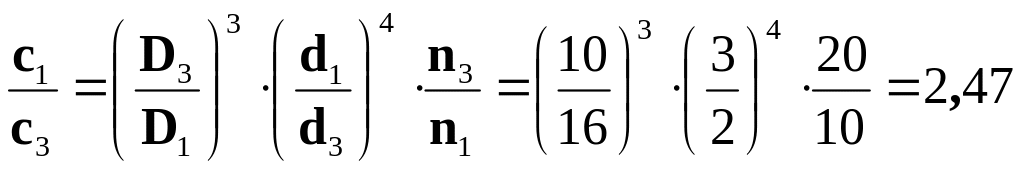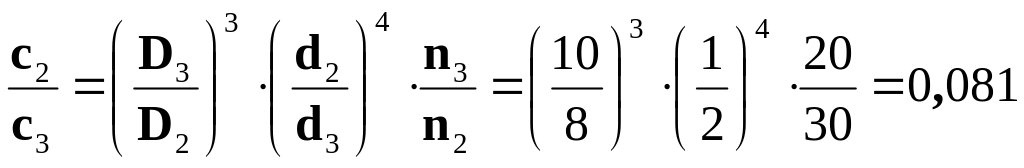Тоді зусилля будуть дорівнювати

Н;

Н;

Н.

Максимальні дотичні напруження в пружинах знаходимо за формулою

.

Визначимо полярні моменти опору поперечних перерізів пружин

м³,

м³,

м³.

Поправочний коефіцієнт k визначається за формулою

.

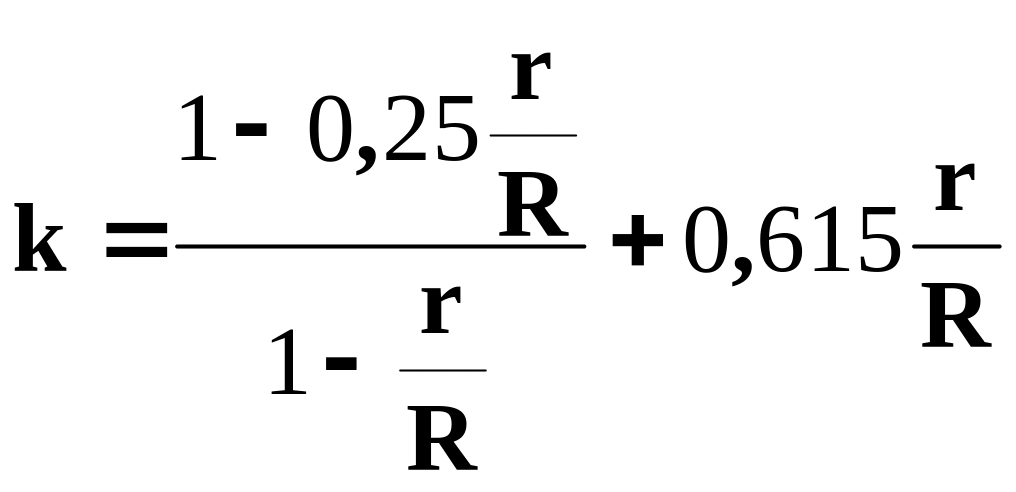Тоді для k₁, k₂, k₃ будемо мати такі значення:

;

;

.

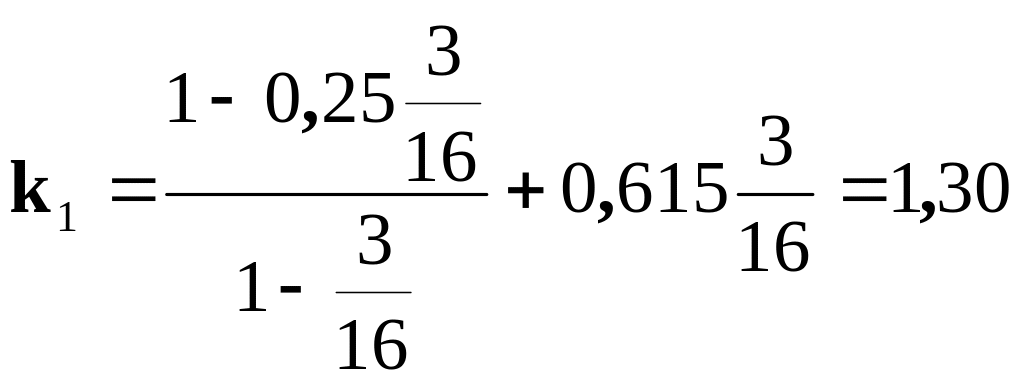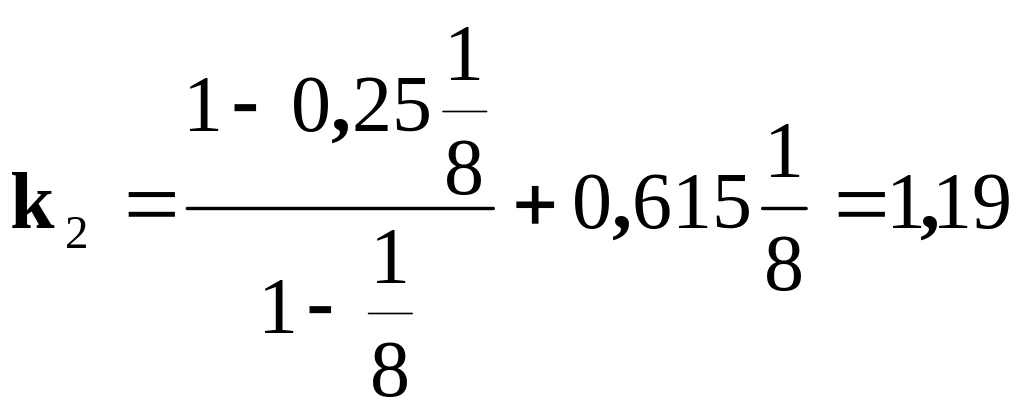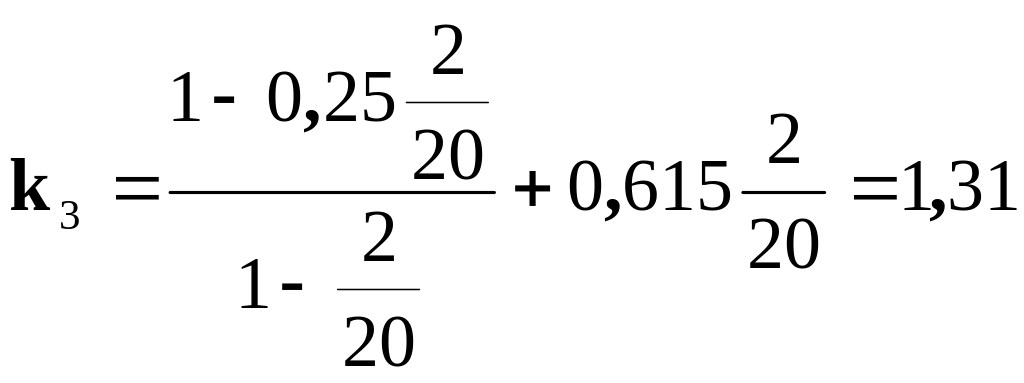Максимальні дотичні напруження у витках пружини дорівнюють, відповідно

МПа;

МПа;

МПа.

Осадку λ в точці А пружини визначаємо за формулою

, де .

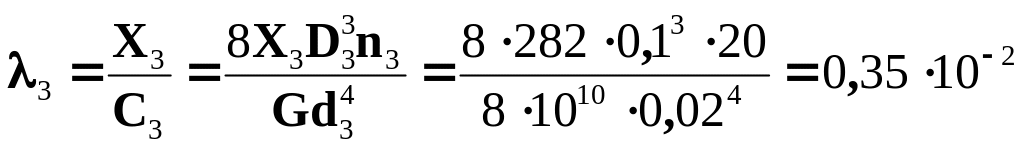Тоді м.

Для перевірки знаходимо подовження пружин 1 і 2, які повинні дорівнювати осадці точки А:

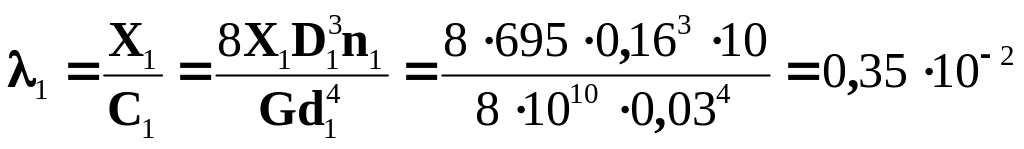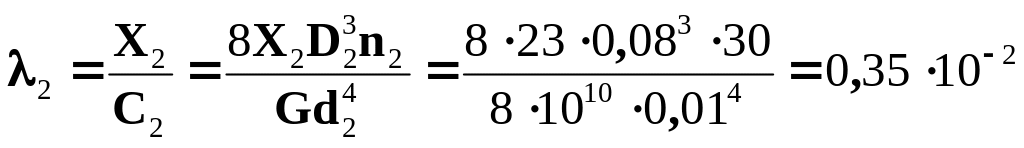м.

м.

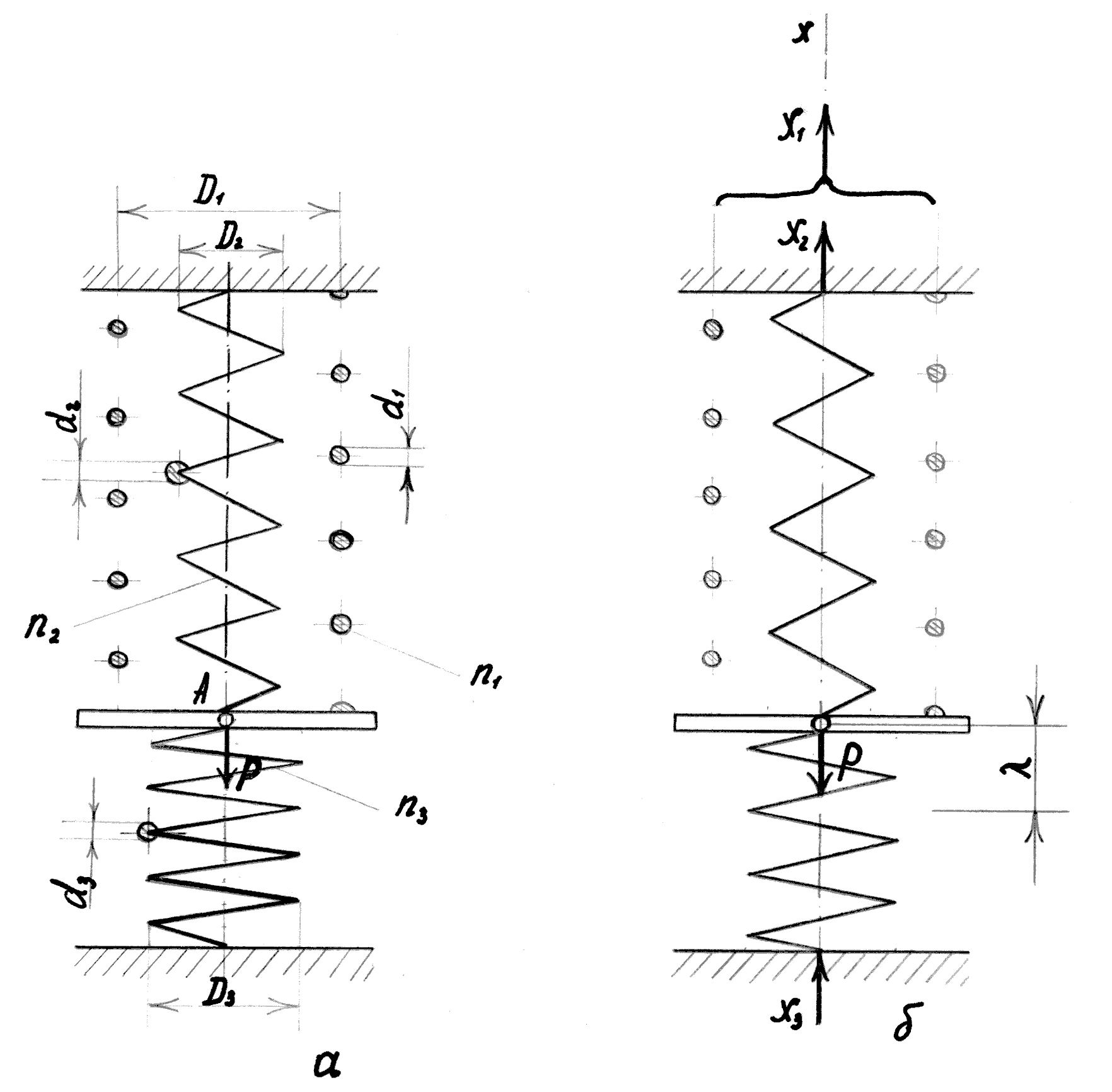
Рис.6.8

Задача 6.6. Кінці круглого стержня жорстко закріплені. Стержень закручується рівномірно розподіленими моментами інтенсивністю (рис.6.9,а). Треба побудувати епюри θ(х) і φ(х).

Розв’язання. Задача, що розглядається, статично невизначувана. В даному випадку запишемо такі вирази:

;

.

При х=0 і при х=ℓ φ=0. Звідки ; С₂=0.

Тоді ;

.

Епюри θ(х) і φ(х) побудовані на рис.6.9 б,в, а епюра М_к – на рис.6.9 г.

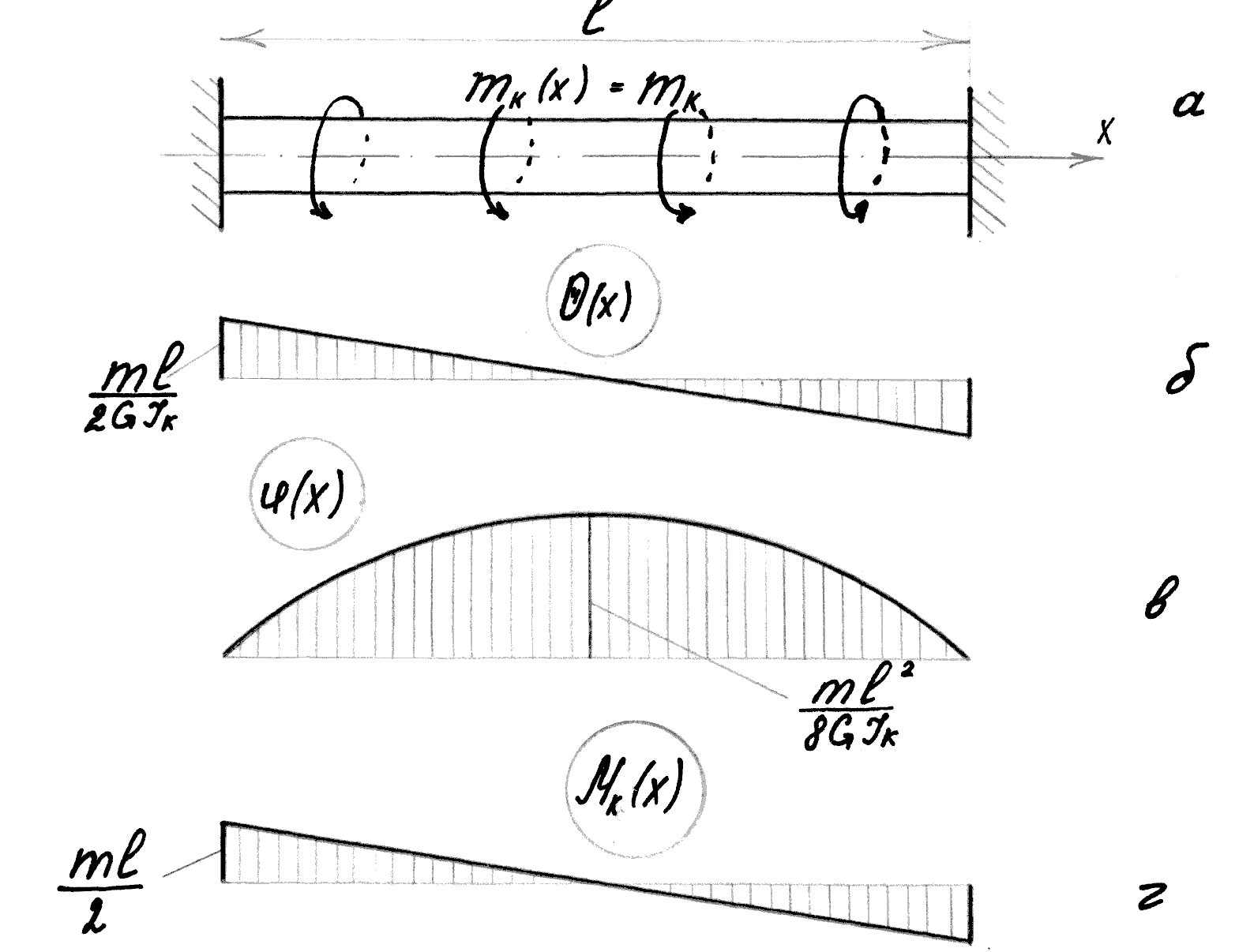
Рис.6.9

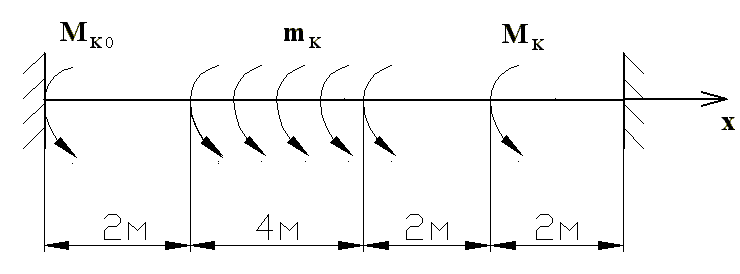
Задача 6.7. Вал, жорстко закріплений двома кінцями і навантажений, як показано на рис.6.10. Нехай m_K=20 кн/м, М_К=80 кн м, GI_к=const. Згідно методу початкових параметрів записати вираз для кута закручування φ(х).

Рис.6.10

Розв’язання. Вибираємо початок координат у лівого затиснення. Початковий параметр φ₀=0. Другий початковий параметр М_К0 знайдемо з граничної умови: φ(ℓ)=0, тобто на другому кінці стержня кут закручування також дорівнює нулю.

Запишемо вираз для кута закручування на останній ділянці при 8≤х≤10:

,

де а=8; b=2; c=6.

Тоді при х=10 м отримаємо рівняння

Із цього рівняння знаходимо М_К0.

М_К0=32 кн м.