Тема4. Геометричні характеристики плоских перерізів.

Лекція 7. Статичний момент плоскої фігури. Моменти інерції плоскої фігури. Формули переходу до паралельних осей. Формули переходу до повернутих осей. Головні осі інерції та головні моменти інерції перерізу. Радіуси інерції. Моменти опору.

Щоб визначити напруження і деформації розтягнутого (стиснутого) стержня, треба знати площу його поперечного перерізу. При вивченні кручення і згину ми маємо справу з новою характеристикою поперечного перерізу бруса – моментом інерції. При визначенні прогину балки під дією вантажу Р, необхідно зазначити, як покладена балка на опори – плазом чи на ребро. Якщо балка лежить на опорах плазом, то прогин від сили Р буде значно більшим, ніж тоді, коли балка покладена на ребро. Площа поперечного перерізу балки не змінилась від того, як вона була покладена на опори, а прогин змінився.

Отже, тут прогин залежить не від площі поперечного перерізу балки, а від іншої характеристики – моменту інерції. Тому перед вивченням згину та кручення слід ознайомитися з моментами інерції, повторити з підручника статики матеріал про статичний момент площі фігури і про знаходження центра ваги плоских фігур.

1

Рис. 4.1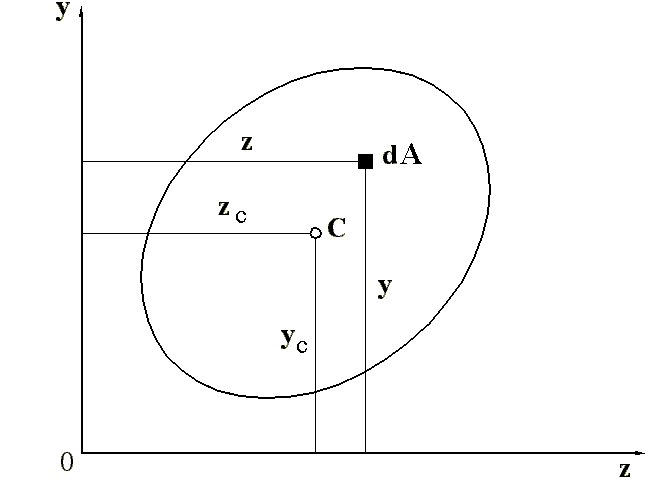

. Статичний момент плоскої фігури. Моменти інерції плоскої фігури. Як першу з геометричних характеристик розглянемо статичний момент плоскої фігури. Статичним моментом плоскої фігури відносно осі y, який позначається через S_y, називається величина .

Статичним моментом цієї ж фігури відносно осі z буде .

Формули для визначення положення центра ваги фігури в прямокутній системі координат Oyz (рис.4.1) запишемо так: .

2. Осьовими моментами інерції I_z та I_y перерізу відносно будь-яких осей z та y (рис.4.2), що лежать у площині перерізу, називаються інтеграли виду

де z та y – відстані від центра елементарної площадки dA до осей y та z.

Р

Рис. 4.2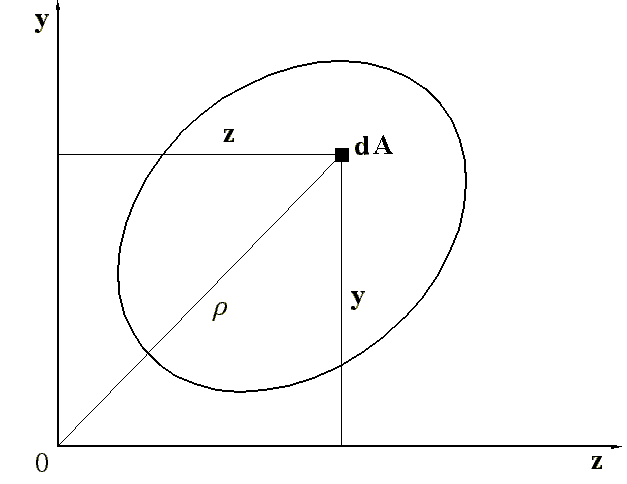

озмірністю статичного моменту плоскої фігури є одиниця довжини у третьому степені.

Полярним моментом інерції I_ перерізу називається інтеграл виду  - відстань від центра елементарної площадки dA до осі, перпендикулярної до площини перерізу (точка O).

Між полярним моментом інерції та осьовими існує залежність .

Відцентровим моментом інерції I_yz перерізу відносно осей z та y називається інтеграл виду .

3

Рис. 4.3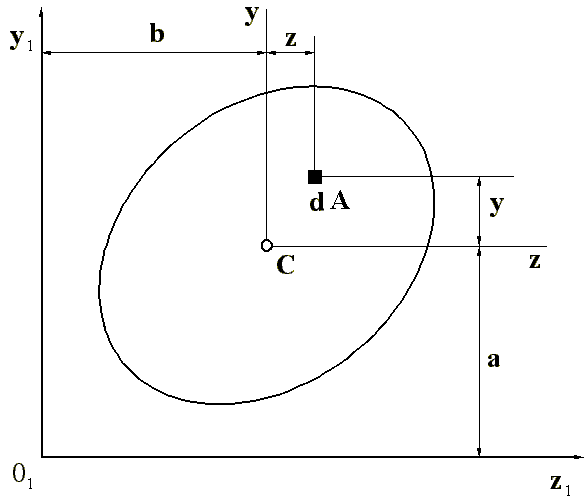

. Формули переходу до паралельних осей. При перенесенні осей координат найменшим із моментів інерції відносно кількох паралельних осей є момент інерції відносно тієї осі, яка проходить через центр ваги.

Нехай система координат Суz (рис.4.3) проходить через центр ваги перерізу, а друга система Oy₁z₁ паралельна їй, тоді:

де a та b – відстані між відповідними осями.

Для відцентрового моменту інерції перерізу маємо формулу .

4

Рис. 4.4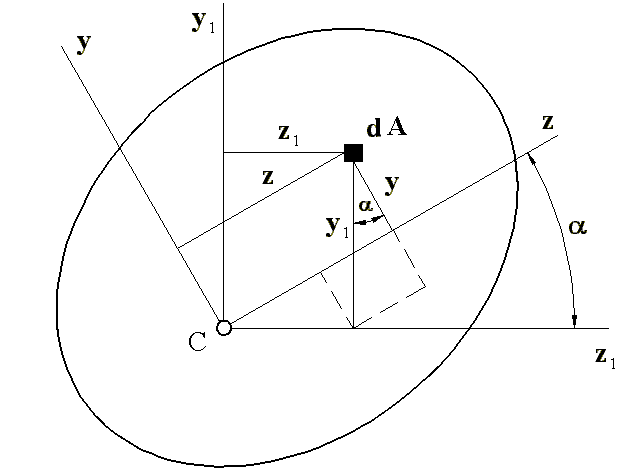

. Формули переходу до повернутих осей. Нехай система координат Сyz, повернута відносно системи координат Cy₁z₁ на кут α (рис.4.4) проти годинникової стрілки. При повертанні осей моменти інерції відносно них змінюються. Отже, моменти інерції відносно осей y і z можна визначити через моменти інерції відносно осей y₁ і z₁ за формулами

; (1)

.

Для відцентрового моменту інерції формула переходу набуває вигляду

. (2)

5. Головні осі інерції та головні моменти інерції перерізу. Центральні осі, відносно яких момент інерції площі перерізу набуває найбільшого і найменшого значення, називають головними центральними осями. Відносно головних осей відцентровий момент інерції дорівнює нулю. Через будь-яку точку в площині фігури можна провести такі дві взаємно перпендикулярні осі, відносно яких відцентровий момент інерції дорівнюватиме нулю.

Використовуючи умову I_yz=0, знайдемо положення головних центральних осей інерції

. (3)

Рівняння (3) має у границях 0÷π два корені: гострий і тупий кути α₀, які відрізняються на . Додатні кути α₀ відкладаються проти ходу стрілки годинника.

Головні моменти інерції, визначені відносно головних центральних осей фігури, дорівнюють

. (4)

Слід зазначити, що формули для головних моментів інерції (4) мають однаковий вигляд із формулами для головних напружень при плоскому напруженому стані. Якщо Iz₁>Iy₁, то головна вісь нахилена до осі z₁ під гострим кутом α₀, визначеним за формулою (3), буде віссю максимального моменту інерції.

6. Радіуси інерції. Моменти опору. Радіусом інерції перерізу (рис. 4.1) називається величина виду , звідки , тобто момент інерції відносно будь-якої осі дорівнює площі перерізу, помноженій на квадрат радіуса інерції відносно тієї ж осі.

Осьовим моментом опору перерізу називається частка від ділення головного моменту інерції на відстань від осі до найбільш віддаленої від неї точки перерізу.