5. Повзучість і релаксація.

З впливом часу зв’язана так звана післядія, яка може виникати в галузі як пружних, так і залишкових деформацій. Практичне значення має післядія в галузі залишкових деформацій, де вона проявляє себе у вигляді повзучості і релаксації.

Порівняно повільне зростання пластичних деформацій в часі при сталому напруженні називається повзучістю. Повзучість залежить від матеріалу і величини напружень. Із збільшенням напружень повзучість зростає.

Релаксацією називається зменшення в часі напружень при сталій величині деформації тіла.

Повзучість і релаксація зростають з підвищенням температури і для сталей має практичне значення лише при підвищених температурах. Для високополімерних пластмас релаксація спостерігається уже при кімнатній температурі.

Реологія – це розділ фізики, який вивчає деформування і текучість матеріалів. У теоретичній частині вона має справу з реологічними тілами, під якими, звичайно, розуміють суцільні середовища, наділені певним комплексом ідеалізованих фізичних властивостей: пружності, пластичності, в’язкості. Механіка спадкових середовищ оперує моделями, що описують властивості реальних матеріалів, у першу чергу, властивості релаксації і повзучості.

На основі обробки експериментальних даних для конкретного матеріалу можна одержати характерну криву повзучості. Для металів така крива показана на рис. 2.5. Вона дає залежність між деформацією і часом, її можна використати для розрахунків.

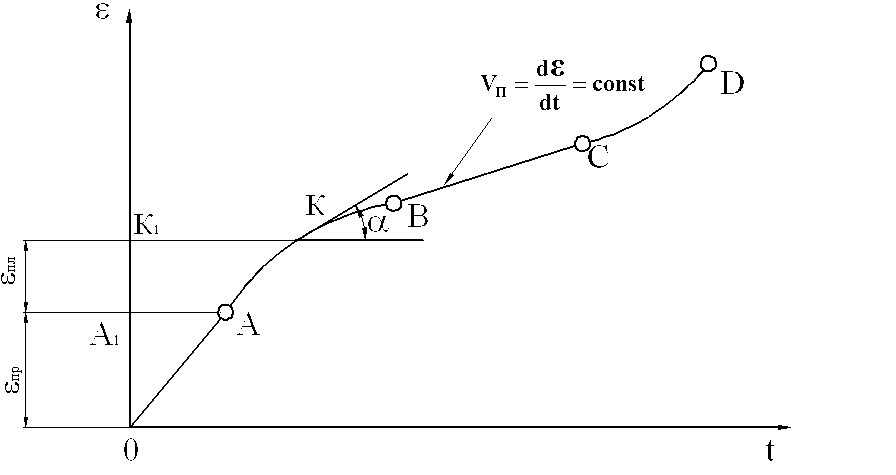
Рис.2.5

Перша (прямолінійна) ділянка ОА цієї кривої – ділянка початкової пружної деформації, що не залежить від часу; ділянка АВ (криволінійна) ділянка неусталеної повзучості, коли повзучість зростає із зменшуваною швидкістю ; ділянка ВС - ділянка усталеної повзучості, де швидкість υ_п=const (ділянка прямолінійна); нарешті, ділянка СD – ділянка швидкого розвитку повзучості, що призводить до зруйнування навантаженого елемента конструкції.

Спрощений закон повзучості для пружнов’язкого матеріалу отримаємо, коли продовжимо ділянку ВС усталеної повзучості до осі координат і сумістимо з цією віссю першу ділянку, ігноруючи криволінійну ділянку АВ. Тоді можна виразити спрощений закон повзучості у вигляді диференційного рівняння, що зв’язує деформацію з часом:

, (4)

де - похідні по t,

t –час;

E –тривалий модуль пружності;

Н –називають миттєвим модулем пружності;

n –називають часом релаксації.

Реологічне рівняння (4) описує модель Кельвіна (реологічне тіло Кельвіна називають стандартним лінійним тілом).

Треба відзначити, що при дуже повільних процесах деформування в рівнянні (4) швидкостями і можна знехтувати в порівнянні із величинами σ і ε, і тоді ми прийдемо до звичайного закону Гука із тривалим модулем пружності Eε=σ. (5)

При дуже швидких процесах деформування, навпаки, швидкості деформацій і напружень дуже великі, і в порівнянні з ними можна знехтувати самими деформаціями ε і напруженнями σ. При цьому знову знаходимо закон Гука, але продиференційований (за часом) із миттєвим модулем пружності Н: (6)

Тут у всіх випадках Н>Е. Окрім рівняння (4) для розв’язання задач деформування, з часом необхідно мати початкові умови, які визначаються через початкові значення напружень і деформацій:

при t=0 ε(0)= ε₀; σ(0)= σ_0.

а) Розглянемо розрахунковий випадок коли σ=const.

Тоді розв’язок рівняння (4) набирає вигляду

.

Із початкових умов маємо

,

тоді знайдемо

. (7)

Величина , оскільки H>E. У зв’язку з цим залежність ε від t має вигляд, показаний на рис.2.6

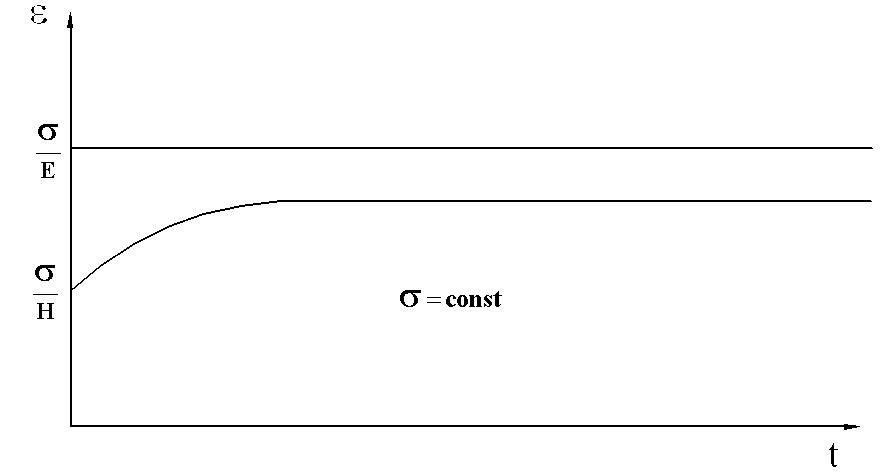
Рис.2.6

Графік повзучості (рис.2.6) відповідає розв’язку (7).

В момент прикладання початкового напруження σ відбувається “стрибок” деформації на величину , що відповідає першій ділянці спрощеної діаграми для реального матеріалу на рис.2.5. У зв’язку з цим величину Н, що визначає деформацію в момент прикладання навантаження, називають миттєвим (початковим) модулем пружності. На графіку (рис.2.6) деформація ε прямує з часом до деякого сталого значення .

б) Якщо деформація ε у навантаженому елементі внаслідок умов його закріплення не може змінити свої величини (ε=const), то розвиток деформації повзучості ε_п відбувається за рахунок зменшення пружної деформації ε_пр із збереженням сталості суми цих деформацій ε_п+ ε_пр=const.

Внаслідок зменшення пружної деформації в елементі знижується зв’язане з нею напруження. Це зниження має назву релаксації (послаблення напружень).

У цьому розрахунковому випадку при ε=ε₀=const розв’язок рівняння (4) набуває вигляду

σ=Еε₀+(σ₀-Еε₀)е^-t/n . (8)

Треба зазначити, що при t→∞ напруження σ згідно рівняння (8) прямує до деякої величини Еε₀ (рис.2.7).

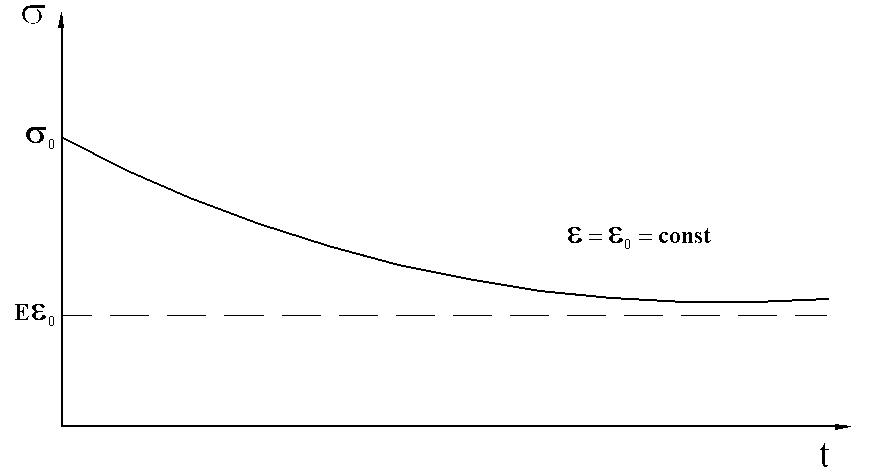
Рис.2.7

Повзучість треба враховувати для металевих конструкцій, що працюють при високій температурі. При цьому розвиток деформацій повзучості перешкоджає нормальній роботі конструкції протягом всього строку роботи, а також може призвести до їх зруйнування.

Наведемо простий спосіб розрахунку на повзучість по граничній сумарній деформації.

Розрахункове рівняння запишемо так:

ε₀+ν_пt_д≤ε_гр , (9)

де ν_п – швидкість усталеної повзучості;

ε₀=ε_пр+ ε_п - сума пружної деформації і деформації усталеної повзучості;

t_д- строк служби деталі;

ε_гр- найбільша гранична деформація (встановлюється технічними умовами), яка допускається за час служби деталі при новій температурі (так звана границя повзучості).

Швидкість ν_п можна виразити емпіричною формулою

ν_п=Кσⁿ , (10)

де

,

або враховуючи вираз (9)

(11)

де σ_гр –найбільше напруження, що відповідає деформації ε_гр.

При розрахунку на повзучість треба здійснити перевірку міцності з урахуванням тривалої дії навантаження при даній температурі за формулою

, (12)

де - границя тривалої міцності, тобто найбільше напруження, яке при заданій сталій температурі викликає руйнування матеріалу в кінці заданого відрізка часу (заданого строку служби деталі);

К_t- коефіцієнт запасу тривалої міцності.

Коефіцієнти К,n - визначаються експериментально.