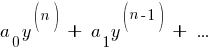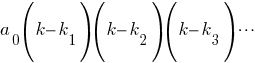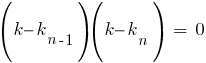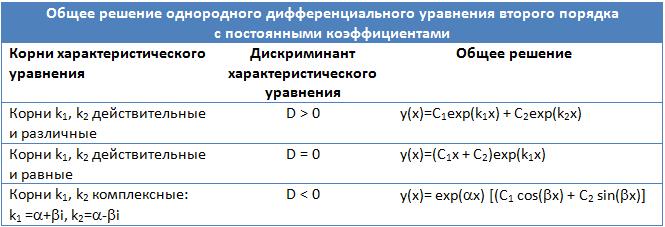
Решение линейных однородных ду с постоянными коэффициентами

Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами:

(1)

Его решение можно получить следуя общему методу понижения порядка.

Однако проще сразу получить фундаментальную систему n линейно независимых решений и на ее основе составить общее решение. При этом вся процедура решения сводится к следующим шагам.

Ищем решение уравнения (1) в виде e^kx. Получаем характеристическое уравнение:

(2)

Оно имеет n корней. Решаем уравнение (2) и находим его корни k_i. Тогда характеристическое уравнение можно представить в виде:

(3)

Каждому корню соответствует одно из линейно независимых решений y_i фундаментальной системы решений уравнения (1). Тогда общее решение уравнения (1) имеет вид:

Решение линейных неоднородных ДУ с постоянными коэффициентами

Установление вида частного решения

Составим характеристическое уравнения однородного уравнения (3):

(4)

Пусть k_i - корни характеристического уравнения (4).

Комплексные корни выразим через действительную и мнимую части:

Для действительных корней k_2i = 0.

Если среди корней k_i нет значения

то частное решение имеет вид:

где s - наибольшее из s₁ и s₂;

многочлены степени s с коэффициентами A_i, B_i, которые подлежат определению подстановкой в уравнение (2).

Если среди корней k_i есть корень

кратности m, то частное решение имеет вид:

После того как установлен вид частного решения, подставляем y₁ в уравнение (2) и находим неизвестные коэффициенты A_i и B_i. После чего получаем общее решение уравнения (2):

Далее рассмотрен пример решения неоднородного дифференциального уравнения со специальной неоднородной частью.

Частные случаи

Неоднородность в виде многочлена

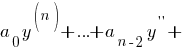
В этом случае α = β = 0.

Если среди корней k_i нет значения

то частное решение имеет вид:

Если среди корней k_i есть корень

кратности m, то частное решение имеет вид:

Неоднородность в виде экспоненты

В этом случае β = 0.

Если среди корней k_i нет действительного значения

то частное решение имеет вид:

Если среди корней k_i есть корень

кратности m, то частное решение имеет вид:

Неоднородность в виде синусов и косинусов

В этом случае α = 0.

Если среди корней k_i нет чисто мнимого значения

то частное решение имеет вид:

Если среди корней k_i есть корень

кратности m, то частное решение имеет вид:

Найти общее решение уравнения  y'' + y' −6y = 36x.

Решение.

Воспользуемся методом неопределенных коэффициентов. Правая часть заданного уравнения представляет собой линейную функцию  f(x) = ax + b. Поэтому будем искать частное решение в виде

     

Производные равны:

     

Подставляя это в дифференциальное уравнение, получаем:

     

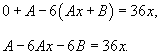
Последнее уравнение является тождеством, то есть справедливо для всех x, поэтому приравняем коэффициенты при слагаемых с одинаковыми степенями x в левой и правой части:

     

Из полученной системы находим: A = −6, B = −1. В результате, частное решение записывается в виде

     

Теперь найдем общее решение однородного дифференциального уравнения. Вычислим корни вспомогательного характеристического уравнения:

     

Следовательно, общее решение соответствующего однородного уравнения имеет вид:

     

Итак, общее решение исходного неоднородного уравнения выражается формулой