Расчет фондов удобрений, отнесенных на прирост урожая, т физ. Веса

вариант	Фонды удобрений под урожай планового периода в ассортименте поставки						Потребность в удобрениях под исходный урожай, скорректированная на последствие удобрения предшественника						Подлежит распределению под прирост урожая
1	Аммиачная селитра	карбамид		суперфосфат	Калийная соль	Аммиачная селитра		карбамид		суперфосфат		Калийная соль	Аммиачная селитра		карбамид		суперфосфат		Калийная соль
1	2	3		4	5	6		7		8		9	10		11		12		13
3	26,0	1,8	57,8		28,8		16,26		-		35,17	7		9,7		1,8		22,63		21,76

Таблица 3

Расчет показателя выхода продукции, отнесенной на исходную урожайность

Участок	Площадь, га	Культура	«Стартовая» урожайность, ц/га	Выход продукции за счет «стартовой» урожайности по всей площади, т
1	2	3	4	5
3	53	Ячмень	18	95,4
4	71	Озимая пшеница	22	156,2
Всего	124	-	-	251,6

Таблица 4

Обеспечение заданных объемов производства продукции

Вариант	Задание по производству продукции, т
	Всего		Из них
			Выполняется за счет исходного урожая			Подлежит выполнению за счет прироста урожая
	ячмень	Озимая пшеница	ячмень		Озимая пшеница	ячмень	Озимая пшеница
1	2	3	4	5		6	7
1	169,5	169,5	95,4	156,2		74,1	13,3

4. Решение экономико-математической задачи распределения фондов минеральных удобрений сельскохозяйственной организации по полям севооборотов и кормовым угодьям.

Разработанная экономико-математическая модель может быть решена симплексным методом, так кая является задачей линейного программирования. Общий принцип, которых таков: выбирается неоптимальный опорный план и его параметры варьируются с целью последовательного улучшения плана, т.е. оптимизации целевой функции при соблюдении всех ограничений, что дает возможность решать оптимизационные задачи.

Рассмотренная задача решена с использованием приложения Поиск решения MS Excel.

Рис.1 Фрагмент рабочего листа MS Excel c исходными данными по участку №1.

Рис.1 Фрагмент рабочего листа MS Excel c исходными данными по участку №1(продолжение)

Рис.2. Фрагмент рабочего листа MS Excel c исходными данными по участку №2 и ограничениями связующего блока по фондам удобрений и заданиям по производству продукции

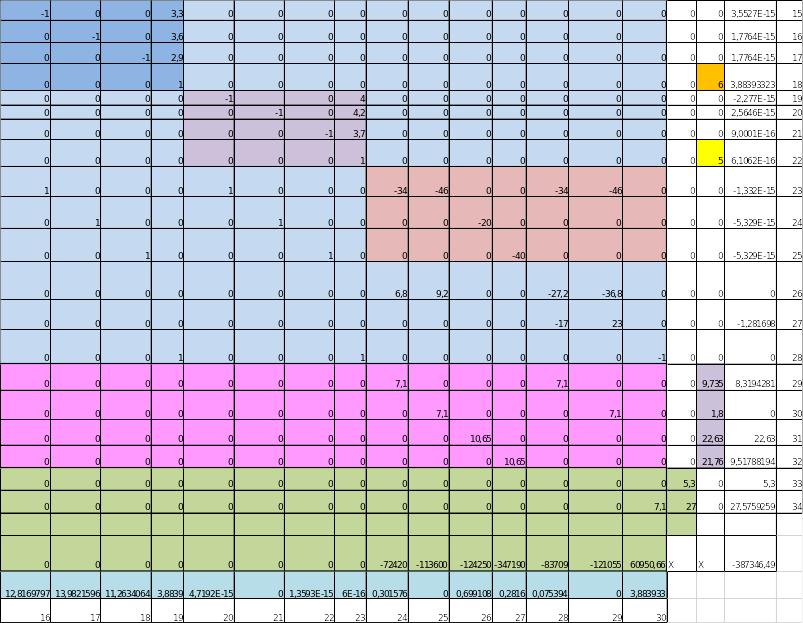
Рис.2а. Фрагмент рабочего листа MS Excel c исходными данными по участку №2 и ограничениями связующего блока по фондам удобрений и заданиям по производству продукции (продолжение)

По результатам решения получены дозы внесения удобрений по различным культурам, в установленные сроки, приросты урожайности культур по интервалам внесения и общий прирост урожайности и величина дополнительного чистого дохода (см. рис.3.).

Рис.3. План распределения фондов удобрений сельскохозяйственного предприятия по полям севооборотов и кормовым угодьям.

Внешний вид экономико-математической модели по распределению фондов минеральных удобрений сельскохозяйственного предприятия по полям севооборотов и кормовым угодьям представлен в приложении 1.