6 Сдвиг.

Под сдвигом понимают такой вид деформации, когда в поперечных сечениях стержня действует только перерезывающая (поперечная сила , ) сила, а остальные силовые факторы отсутствуют.

Такое нагружение соответствует действию на стержень двух равных противоположно направленных и бесконечно близко расположенных поперечных сил (рис. 4.8, а, б), вызывающих срез по плоскости, расположенной между силами (как при разрезании ножницами прутков, листов и т. п.).

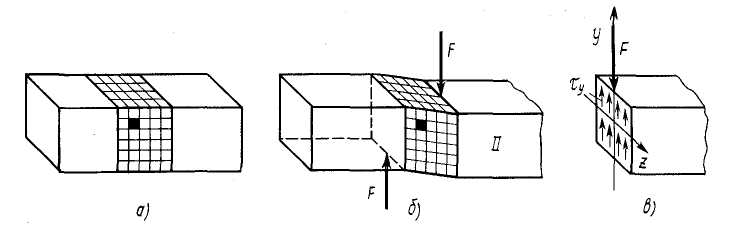
Рис. 4.8. Схема деформации и внутренние силы при сдвиге стержня

Сдвигу предшествует деформация – искажение прямого угла между двумя взаимно перпендикулярными линиями (см. сетку линий на поверхности стержня, рис. 4.8, а, б). При этом на гранях выделенного элемента (зачернен на рис. 4.8, а, б) возникают касательные напряжения , вызываемые внутренней перерезывающей силе (рис. 4.9).

Величина называется абсолютным сдвигом, угол на который изменяются прямые углы элемента, называют относительным сдвигом,

.

Зависимость справедлива, так как рассматриваются относительно жесткие тела, у которых упругие деформации малы по сравнению с величиной тела.

Рис. 4.9. Деформация сдвига

Чистым сдвигом называется напряженное состояние, при котором на гранях выделенного элемента действуют только касательные напряжения . Чистый сдвиг эквивалентен растяжению и сжатию элемента в диагональных направлениях.

Экспериментально установлено, что в пределах упругих деформаций величина сдвига пропорциональна сдвигающей силе , расстоянию , на котором происходит сдвиг, и обратно пропорциональна площади сечения . Если ввести коэффициент пропорциональности , зависящий от свойств материала, закон упругости для сдвига выразится формулой

,

где – жесткость сечения при сдвиге.

Между модулями упругости и сдвига существует взаимосвязь

,

здесь – коэффициент Пуассона.

Модуль сдвига

МПа для стали,

МПа для чугуна.

С одной стороны , с другой , тогда или . Принимая, что касательные напряжения равномерно распределены по поперечному сечению площадью , будем иметь , отсюда Закон Гука при сдвиге

– связь касательных напряжений и относительного сдвига.

В результате условие прочности при сдвиге

.

Формула для проектного расчета

.

6. Кручение.

Кручением называется такой вид деформации, при котором в поперечных сечениях вала действует только крутящий моментвнт – чистое кручение.

Рис. 4.10. Деформация кручения

Из рисунка 4.10 видно, что при кручении имеет место взаимный поворот параллельных сечений, ограничивающих выделенный элемент, относительно общей, нормальной к ним оси. Схема деформации аналогична чистому сдвигу. Наиболее простым является решение задачи о кручении стержней кругового профиля. При чистом кручении внутренние силы и соответствующие им напряжения лежат в сечении, то есть являются касательными.

Крутящий момент является статическим эквивалентом внутренних усилий, распределенных по определенному закону:

.

В соответствии с гипотезой плоских сечений поперечные сечения стержня круглого сечения при кручении остаются плоскими и радиусы в поперечных сечениях остаются прямолинейными.

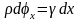Из исунка 4.10 имеем с одной стороны , а с другой . Следовательно и

Согласно закону Гука при сдвиге , и с учетом последней формулы получаем

Так как множитель для всех точек сечения одинаков, следовательно, напряжения прямо пропрциональны радиусу , то есть изменяются по линейному закону.

Выражение для момента можно записать в виде

.

Интеграл является геометрической характеристикой сечения, называемой полярным моментом инерции , то есть . Учитывая, что , получим

, откуда ,

где – полярный момент сопротивления сечения (для круглого стержня , ).

В результате условие прочности при кручении

.

Формула для проектного расчета

.

Угол закручивания

,

где – длина бруса (стержня); – жесткость при кручении.

Условие жесткости при кручении

,

где – допускаемый угол зактучивания погонного метра стержня, рад/м.