Балансировка роторов при различных видах неуравновешенности

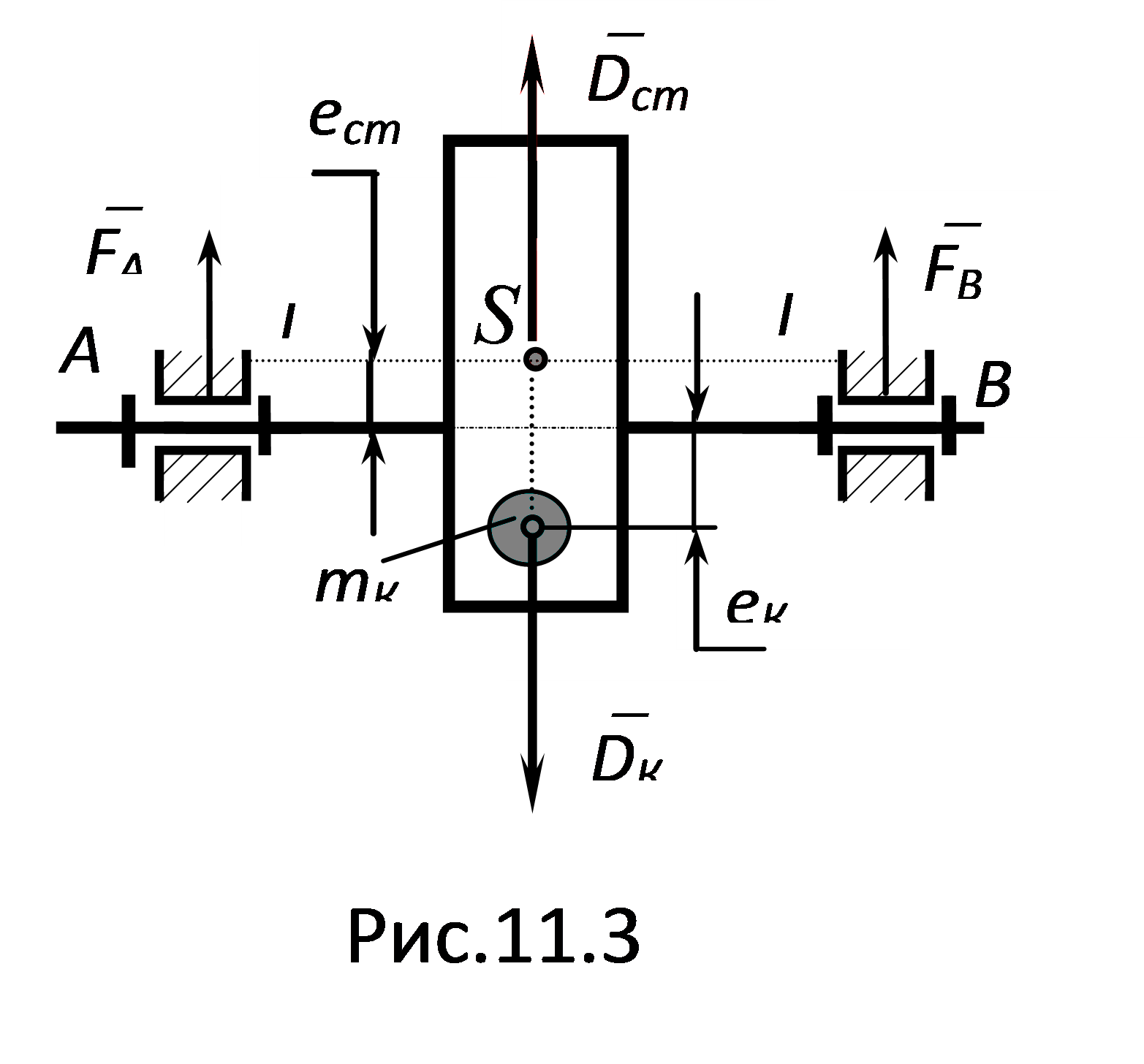
1. Статическая неуравновешенность

Статическая неуравновешенность свойственна такому ротору, центр масс S которого не находится на оси вращения, но главная центральная ось инерции (I - I) которого параллельна оси вращения. В этом случае е_ст  0, и главный вектор дисбалансов D_ст  0. Главный момент дисбалансов ротора M_D = 0. Статическая неуравновешенность выражается только главным вектором дисбалансов. Он направлен радиально и вращается вместе с ротором.

Примером может служить коленчатый вал одноцилиндровой машины, ротор крыльчатки со смещенной осью вращения.

;

.

Величина может значительно превышать G , если будут значительными  или е_ст. Например: если G =10 H. m = G/g = 1кг, е_ст. = 0,1 мм,  = 100 рад/с, то = 10⁴  1  0,1 = 10³ Н, т.е. в 1000 раз больше статической нагрузки ротора на его опоры.

Статическая неуравновешенность может быть устранена, если к ротору прикрепить добавочную массу m_к, так называемую корректирующую массу. Ее нужно разместить с таким расчетом, чтобы . Корректирующая масс определяется: m_k = D_k / e_К , где величиной e_К задаются из соображений удобства размещения противовесов. Направление вектора D_К противоположно направлению D_ст. Центр корректирующей массы должен находиться на линии действия вектора D_ст, а вектор e_К должен быть направлен в сторону противоположную е_ст.

Однако статическую балансировку не всегда конструктивно удается выполнить одной корректирующей массой. Так для конструкции одноколенчатого вала применяют две плоскости коррекции, а пространство между этими плоскостями оставляют свободным для движения шатуна. В этом случае .

Обычно , а .

2. Моментная неуравновешенность

Моментная неуравновешенность имеет место в том случае, когда центр масс S находится на оси вращения, а главная центральная ось инерции I-I наклонена к оси вращения ротора под углом  (рис. 11. 4)

В этом случае е_ст = 0, следовательно D_ст = 0, так что моментная неуравновешенность выражается только лишь главным моментом дисбалансов M_D, т.е. парой дисбалансов D_м1 и D_м2, которая вращается вместе с ротором. Примером может служить двухколенчатый вал, для которого M_D =M_D  h. Опоры А и В нагружены парой сил (F_A , F_B), векторы которых вращаются вместе с валом.

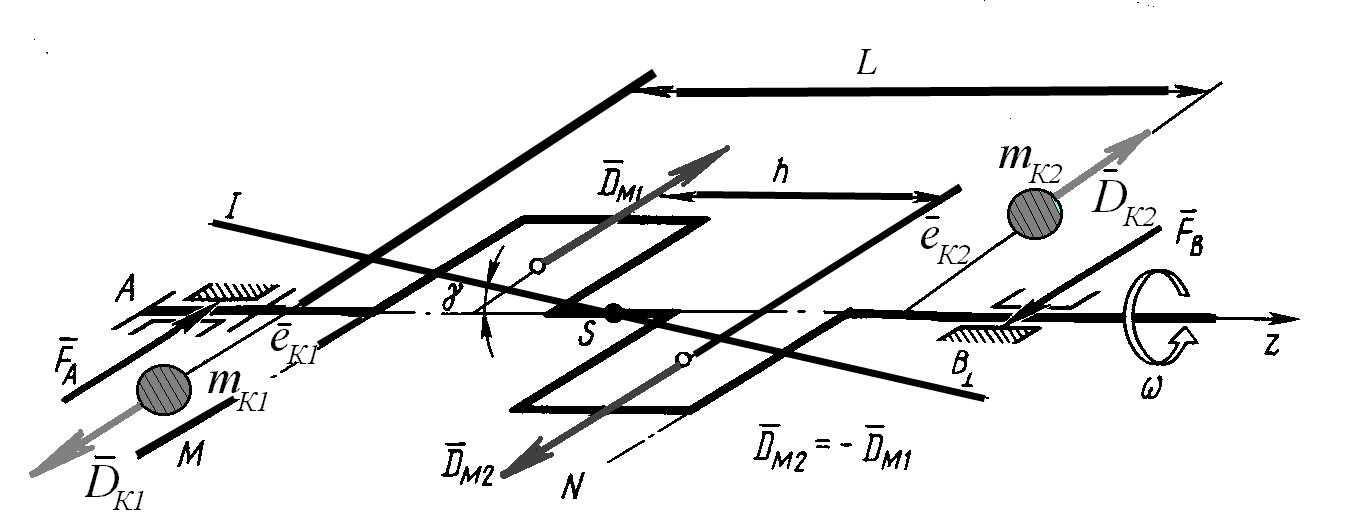Рис. 11. 4

Так как пара сил уравновешивается только парой, то устранить моментную неуравновешенность можно в том случае, если применить не менее чем две корректирующие массы. Их расположение в плоскостях коррекции и их величины должны быть такими, чтобы дисбалансы корректирующих масс m_К1 и m_К2 составили бы именно пару D_К1 и D_К2 . Массы выбираются и размещаются так, чтобы момент их дисбалансов M_DК был по величине равен, а по направлению противоположен моменту дисбалансов ротора: M_Dk = - М_D , M_DК = D_К1 L_К + D_К2  L_К = M_DК1 + M_DК2,

где D_К = m_К e_К .

3. Динамическая уравновешенность

Динамическая уравновешенность является совокупностью двух предыдущих. При динамической неуравновешенности главная центральная ось инерции ëèáî пересекает ось вращения не в центре масс ротора точке S, либо перекрещивается с ней; и главный вектор дисбалансов D_ст , и главный момент дисбалансов М_D не равны нулю (рис. 11. 5):D_ст  0, М_D  0. т.е. необходимо уравновесить вектор D_ст и момент дисбалансов М_D.

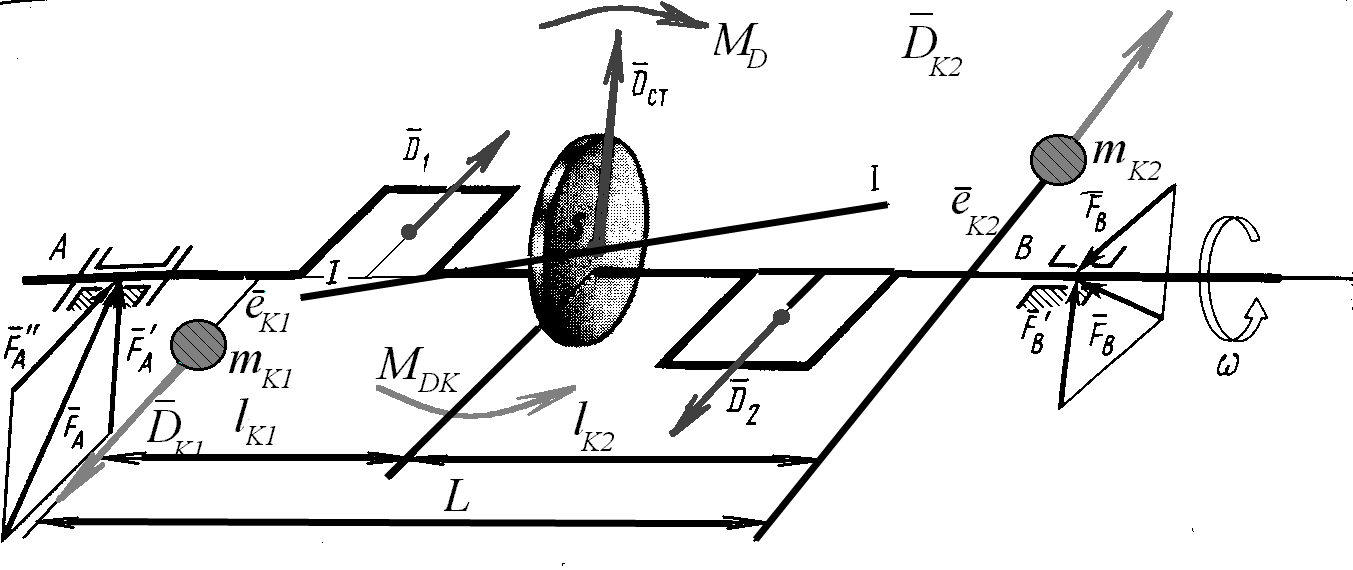Рис. 11. 5

Для этого достаточно разместить на роторе две корректирующие массы m_К1 и m_К2 на расстояниях от оси вращения e_К1 и e_К2 , а от центра масс S, соответственно на l_К1 и l_К2. Массы выбираются и размещаются так, чтобы момент их дисбалансов M_DК был по величине равен, а по направлению противоположен моменту дисбалансов ротора М_D:

M_DК = - М_D , M_DК = D_К1 l_К1 + D_К2  l_К2 = M_DК1+ M_DК2 ,

где D_К1 = m_К1e_К1 и D_К2 = m_К2 e_К2,

а векторная сумма дисбалансов была равна и противоположно направлена вектору D_ст: D_ст = - D_К = - (D_К1 + D_К2 ) .

В этих зависимостях величинами l_Кi и e_Кi задаются из условий удобства размещения противовесов на роторе, а величины m_Кi рассчитывают.

Из вышеизложенного следует, что ликвидация всякой неуравновешенности – и статической, и моментной, и динамической – имеет своим результатом то, что главная центральная ось инерции ротора совмещается с его осью вращения, или аналитически D_ст = 0, М_D = 0 . В этом случае ротор называется полностью сбалансированным. Отметим важное свойство такого ротора: если ротор полностью сбалансирован для некоторого значения угловой скорости, то он сохраняет свою полную сбалансированность при любой другой угловой скорости, как постоянной, так и переменной.