1. Хар-ки прочности стали в расчетах

Принимая за основную характеристику прочности металла временное сопротивление - 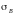, мы тем самым допускаем в конструкции развитие значительных пластических деформаций.

В большинстве случаев чрезмерные пластические деформации приводят к потере несущей способности, поэтому для основной массы металлических конструкций за предельное сопротивление материала принимается предел текучести - .

Для конструкций, в которых развитие пластических деформаций не является препятствием для их дальнейшей работы за предельное сопротивление материала можно принять предел прочности - .

Нормы проектирования устанавливают два значения нормативного сопротивления металла:

• нормативное сопротивление, установленное по пределу текучести - R_уп

• нормативное сопротивление, установленное по пределу прочности - R_ип.

В расчете конструкций используют расчетные сопротивления: R=R^н/ .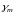

- коэффициент надежности по материалу (учитывает изменчивость механических свойств стали в различных плавках, разные условия работы металла в стандартных образцах и в реальной конструкции и минусовые допуски при прокате)

Численные значения нормативных сопротивлений - R_уп и R_ип и расчетных сопротивлений R_у и R_и приведены в нормах проектирования.

2,3 - Сжатые элементы

1. Сделайте самостоятельно вывод формулы критических напряжений центрально-сжатого стержня.

Критическая сила для упругого, ценрально-сжатого, шарнирно-опертого по концам стержня впервые была определена Л. Эйлером в 1744 году:

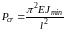, (7.1)

где Е - модуль упругости металла; J_min - минимальный момент инерции сечения стержня; l - длина стержня.

Напряжение, которое возникает в сечении стержня от критической силы, называется критическим напряжением:

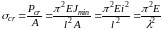, (7.2)

где - площадь поперечного сечения стержня без учета возможных ослаблений; - минимальный радиус инерции стержня; - гибкость стержня.

Для удобства расчетов критическое напряжение выражают через расчетное сопротивление стали – R_у и коэффициент продольного изгиба - :

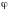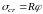. (7.5)

Коэффициент понижает расчетное сопротивление стали до значений критических напряжений - .

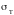- критические напряжения стержня с учетом случайных эксцентриситетов

- предел текучести стали

2. С помощью графической зависимости и поясните, когда стержни теряют устойчивость в упругой стадии работы, а когда в упруго-пластической стадии?

Из (7.2) видно, что величина критического напряжения зависит только от гибкости стержня, так как числитель - величина постоянная в пределах работы стали до напряжений, равных пределу пропорциональности -

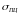
Графически зависимость критических напряжений от гибкости изображается гиперболой. Учитывая, что для обычной малоуглеродистой строительной стали Е = 2,06·10⁵ МПа, а 200 МПа, из (7.2) можно получить наименьшую гибкость, выше которой будет справедлива формула Эйлера

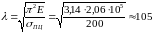. (7.3)

Критические напряжения для стержней малой ( <30) и средней (30< <100) гибкости получаются больше , но меньше (предела текучести) и теоретическое определение критических напряжений таких стержней значительно усложняется, так как потеря устойчивости их происходит при частичном развитии пластических деформаций и переменном значении модуля упругости - Е_пл.

3. Что такое случайный эксцентриситет? Какую роль он играет в работе центрально-сжатого стержня?

Абсолютно прямолинейный стержень является идеализированной расчетной схемой. Все реальные стержни в натуре имеют неизбежные отклонения от прямолинейности (случайные эксцентриситеты). Поэтому любой, так называемый центрально-сжатый стержень, с самого начала работает как внецентренно-сжатый с малым эксцентриситетом. Величина случайных эксцентриситетов определяется статистическим изучением реальных стержней. Конструктивное оформление концов сжатых стержней не обеспечивает идеальную центровку, поэтому эти факторы учитываются введением в расчет эквивалентного эксцентриситета сжимающей силы «e_{f e}»

4. Запишите формулу для проверки устойчивости стержня сжатого осевой силой.

Устойчивость центрально-сжатого стержня будет обеспечена, если напряжения в нем будут меньше критических

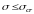. (7.4)

Для удобства расчетов критическое напряжение выражают через расчетное сопротивление стали – R_у и коэффициент продольного изгиба - :

. (7.5)

Формула для проверки устойчивости стержня сжатого осевой силой запишется

, (7.6)

где N = Р - продольное осевое усилие в стержне.

Значение коэффициента можно определить по формулам или по таблицам, приведенным в нормах проектирования. Величина его зависит от расчетного сопротивления стали и гибкости стержня

, (7.7)

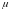где - геометрическая длина стержня; - коэффициент приведения к расчетной длине, величина которого зависит от условий закрепления стержня по концам.

Значения всех параметров в расчетах на устойчивость получены в нормах проектирования на основе унифицированной диаграммы работы материала .