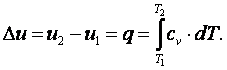Смесь газов. Закон Дальтона.

Остановимся еще вкратце на смеси идеальных газов.

Смесью газов называется совокупность нескольких разнородных газов, которые при рассматриваемых условиях не вступают друг с другом в химические реакции.

Смесь газов – гомогенная термодинамическая система (внутри которой нет поверхностей раздела, отделяющих друг от друга макроскопические части системы, различающиеся по своим свойствам и составу).

Парциальным давлением P_i i-го газа в смеси называется давление, под которым находился бы этот газ, если бы из смеси были удалены все остальные газы, а V и T остались прежними.

Закон Дальтона: в случае идеальных газов сумма парциальных давлений равна давлению всей газовой смеси:                 P = P₁ + P₂ +…+ P_n

                                                                       (8)

аналогично и для парциальных объемов: 

– закон Амага                                                               (9)

При расчете параметров состояния смеси идеальных газов можно пользоваться уравнением Менделеева-Клапейрона в форме:

,                                                                                  (10)

где       М – масса всей системы;

 – кажущийся молекулярный вес.

_{Для реальных газов наблюдаются отступления, которые будут разобраны на более поздних лекциях.}

9. Изохорный процесс (v=const)

Такой процесс может совершаться рабочим телом, находящимся в цилиндре при неподвижном поршне, если к рабочему телу подводится теплота от источника теплоты (см. рис. 4.1) или отводится теплота от рабочего тела к холодильнику. При изохорном процессе выполняется условие dv=0 или v=const. Уравнение изохорного процесса получим из уравнения состояния идеального газа (см. &1.6) при v=const. В pv-координатах график процесса представляет собой прямую линию, параллельную оси p. Изохорный процесс может протекать с повышением давления (процесс 1-2) и с понижением (процесс 1-2’).

Рис. 4.1. График изохорного процесса в p-v координатах

З апишем для точек 1 и 2 уравнения состояния:p₁·v=R·T₁; p₂·v=R·T₂. Следовательно, для изохорного процесса

(4.6)

Приращение внутренней энергии газа

(4.7)

Работа газа

так как dv=0.

Энтальпия газа i_v=u+p·v, а di_v=du+d(p·v)=du+p·dv+v·dp=du+v·dp. Поэтому

(4.8)

Энтропия 

То есть

(4.9)

10. Изобарный процесс (p=const)

В p-v координатах график процесса представляет собой прямую линию параллельную оси v (рис. 4.2). Изобарный процесс может протекать с увеличением объёма (процесс 1-2) и с уменьшением (процесс 1-2’). Запишем для точек 1 и 2 уравнения состояния:p·v₁=R·T₁; p·v₂=R·T₂.

Рис. 4.2. График изобарного процессав p-v координатах

С ледовательно, для изобарного процесса

(4.10)

Приращение внутренней энергии газа  Работа газа   Так как p·v₂=R·T₂, аp·v₁=R·T₁, то l=R·(T₂-T₁). Следовательно, газовая постоянная имеет определённый физический смысл: это работа 1 кг газа в изобарном процессе при изменении температуры на один градус. Из выражения (4.3) следует, что в изобарном процессе q=c_p·(T₂-T₁). В соответствии с первым законом термодинамики для изобарного процесса можно записать dq=du+p·dv= du+d(p·v)=di. Поэтому в изобарном процессеdi=q=c_p·(T₂-T₁). Из соотношений, характеризующих изобарный процесс, вытекает известное уравнение Майера. Так как dq=c_p·dT=c_v·dT+dl=c_v·dT+R·dT, тоR=c_p-c_v.

Используя выражение (4.5), можно показать, что в изобарном процессе энтропия газа

11. Изотермический процесс (T=const)

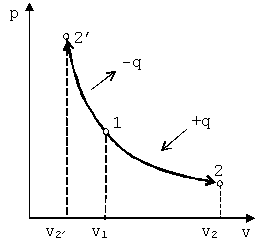
В p-v координатах график процесса изображается равнобокой гиперболой (рис. 4.3). Изотермический процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

Рис. 4.3. График изотермического процесса вp-v координатах

З апишем для точек 1 и 2 уравнения состоянияp₁·v₁=R·T; p₂·v₂=R·T. Следовательно, для изотермического процесса p₁·v₁=p₂·v₂=const.

Приращение внутренней энергии газа

Работа газа

(4.12)

Теплота, подводимая в процессе

(4.13)

Изменение энтальпии газа Δi=Δu+Δ(p·v)=0.

Изменение энтропии газа