Міністерство освіти і науки, молоді та спорту України

Національний університет водного господарства та природокористування

Кафедра електротехніки і автоматики

Звіт

з навчальної практики:

«комп’ютерне моделювання»

Виконав:

Студент 2 курсу

Групи АУТП-21

Олексієвець А.П.

З.к: 311543

Перевірив:

Мельник

Рівне – 2013

Завдання 1

Методи розв'язку алгебраїчних та диференціальних рівнянь та їх систем.

1. Знайти корені або формули коренів для обчислення алгебраїчних (приведених в табл. 1) та диференціальних (приведених в табл. 2) рівнянь та їх систем з допомогою засобів середовища MatLab та аналітично.

2. Порівняти результати, отримані аналітично і за допомогою засобів MatLab та зробити відповідні висновки.

Завдання 1.1.

( Нелінійні алгебраїчні рівняння.)

розв’язати такими способами:

а) аналітично,

Зробити перевірку отриманих результатів

Отримані результати записати у таблиці, зробити висновки.

№				Рівняння
18	43	68	93

Розв’язок аналітично:

[x]=solve('a*(b^2)*(x^2)-x+a=0')

x =

-((1 - 4*a^2*b^2)^(1/2) - 1)/(2*a*b^2)

((1 - 4*a^2*b^2)^(1/2) + 1)/(2*a*b^2)

Знайдемо з допомогою команди solve формули для коренів квадратного рівняння.

Для цього в середовищі MatLab наберемо команду:

[x]=solve('a*log(x)-atan(b*x)=0')

Warning: Explicit solution could not be found.

> In solve at 81

x =

[ emptysym ]

1.2 Остання цифра шифру 3.Вінтегральних схемах використовують планарні конденсатори, що мають вид металічногодиска,розташованого вкругломувирізіметалізаціїна поверхні діелектричноїпідкладки(див. малюнок). Ємність такого конденсатора визначається по формулі:

д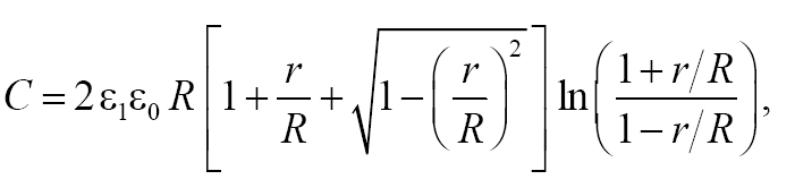 еε₁−відноснадіелектрична проникністьдіелектрика,ε₀=8,85⋅10⁻¹²Ф/м, R − радіус вирізу, r – радіус диска.

Задавшись зазначеними в таблиці параметрамиε₁іr, знайдіть радіусR, що забезпечує необхідну ємність С.

Параметр	Останні цифри шифру
	03	13	23	33	43	53	63	73	83	93
ε1	1	12	10	4	7	6,1	9	2	4	5
r, мм	31	5	3,5	5	4	3	2	3	5	2
С, пФ	4,7	5,5	6	27	36	47	22	22	56	8,1

Розв’язок в MatLab:

[r]=solve(‘2*E1*E0*R(1+r/R+sgrt(1-r/R)^2))log((1+r/R)/(1-r/R)-c’)

Висновок: На прикладі даного завдання, я навчилася обчислювати алгебраїчні рівняння для знаходження фізичних величин з допомогою функції solve в MatLab. Отриманий радіус знаходиться в допустимих межах.

Завдання 1.3.

№	Система рівнянь
3

Завдання 1.3. розв’язати такими способами:

а) аналітично (методом Гауса чи Крамера в EXCEL),

б) з допомогою функції solveMatlab,

в) командним способом в Matlab.

Зробити перевірку отриманих результатів

Отримані результати записати у таблиці, зробити висновки.

Excel(Метод Крамера):

Матриця			Вільні члени
-1,32	2,15	7,6	-1,4
2,62	6,1	-4,12	5,6
8,3	-2,84	-1,5	-6,5
Матриця 1
-1,4	2,15	7,6
5,6	6,1	-4,12
-6,5	-2,84	-1,5
Матриця 2
-1,32	-1,4	7,6
2,62	5,6	-4,12
8,3	-6,5	-1,5
Матриця 3
-1,32	2,15	-1,4
2,62	6,1	5,6
8,3	-2,84	-6,5		x1=		-0,59575
				x2=		0,822461
				x3=		-0,52035

З допомогою функції solveMatlab:

>> [x1,x2,x3]=solve('-1.32*x1+2.15*x2+7.6*x3=-1.4','2.62*x1+6.1*x2-4.12*x3=5.6','8.3*x1-2.84*x2-1.5*x3=-6.5')

x1 =

-0.59575174368302442937448005993164

x2 =

0.82246137921276798111113177940937

x3 =

-0.52035319302224255344253250063683

Командним способом Matlab:

f0=[5.1;4.2;-1.2];

f1=[1.5;1.2;0.5];

f2=[-0.8;7.18;-1.5];

f3=[4.25;-3.2;7.1];

F=[f1 f2 f3]

F =

1.5000 -0.8000 4.2500

1.2000 7.1800 -3.2000

0.5000 -1.5000 7.1000

>>f0=[-1.4;5.6;-6.5];

>>f1=[-1.32;2.62;8.3];

>>f2=[2.15;6.1;-2.84];

>>f3=[7.6;-4.12;-1.5];

>>F=[f1 f2 f3]

F =

-1.3200 2.1500 7.6000

2.6200 6.1000 -4.1200

8.3000 -2.8400 -1.5000

>> d=det(F)

d =

-478.8869

>> F1=[f0 f2 f3]

F1 =

-1.4000 2.1500 7.6000

5.6000 6.1000 -4.1200

-6.5000 -2.8400 -1.5000

>> d1=det(F1)

d1 =

285.2977

>> F2=[f1 f0 f3]

F2 =

-1.3200 -1.4000 7.6000

2.6200 5.6000 -4.1200

8.3000 -6.5000 -1.5000

>> d2=det(F2)

d2 =

-393.8660

>> F3=[f1 f2 f0]

F3 =

-1.3200 2.1500 -1.4000

2.6200 6.1000 5.6000

8.3000 -2.8400 -6.5000

>> d3=det(F3)

d3 =

249.1903

>>x1=d1/d

x1 =

-0.5958

>> x2=d2/d

x2 =

0.8225

>> x3=d3/d

x3 =

-0.5204

	Аналітичне виконання за допомогою методу Крамера	Виконання з допомогою засобів середовища MatLab, команда solve	Виконання з допомогою засобів середовища MatLab командним способом
Х1	-0,59575	-0.5957517	-0.5958
Х2	0,822461	0.8224613	0.8225
Х3	-0,52035	-0.5203531	-0.5204

Висновок: На прикладі даного завдання, я обчислювала системи диференціальних рівняння з допомогою Matlab, а також згадала з курсу вищої математики, як аналітично розв’язуються системи диференціальних рівняння методом Крамера. Отримані розв’язки системи диференціальних рівняння, зробленого двомаспособами співпали, отже можна зробити висновок, що дана система розв’язана правильно.

Завдання 1.4.

Варіанти завдань. Побудувати графік і вивести у вигляді таблиці розв’язокзадачі Коші на інтервалі [0; 1] методом Рунге-Кутта 4-го порядку. Дані взяти з таблиці 2.

Таблиця 2

№ п/п	f(x,y)	уо
13.		0.5

Розв’язок:

М-Файл оформляється :

functiondydx=F(x,y)

dydx=zeros(1,1);

dydx(1)=exp(-y)-exp(x)-0.1

end

Чисельний розв’язок задачі Коші:

>>[X Y]=ode45(@F,[0 1],[1 5])

>> [X,Y]

ans =

X =	Y =
0 0.1000	0.0050 0.1050
0.0100 0.1100	0.0151 0.1151
0.0201 0.1201	0.0451 0.1451
0.0701 0.1701	0.0951 0.1951
0.1201 0.2202	0.1451 0.2453
0.1701 0.2705	0.1951 0.2957
0.2201 0.3210	0.2451 0.3465
0.2701 0.3721	0.2951 0.3978
0.3201 0.4238	0.3451 0.4499
0.3701 0.4764	0.3951 0.5031
0.4201 0.5301	0.4451 0.5576
0.4701 0.5854	0.4951 0.6137
0.5201 0.6425	0.5451 0.6718
0.5701 0.7017	0.5951 0.7323
0.6201 0.7636	0.6451 0.7956

0.5201 0.6425	0.5451 0.6718
0.5701 0.7017	0.5951 0.7323
0.6201 0.7636	0.6451 0.7956
0.6701 0.8285	0.6951 0.8622
0.7201 0.8968	0.7451 0.9325
0.7701 0.9691	0.7951 1.0069
0.8201 1.0459	0.8451 1.0860
0.8701 1.1275	0.8951 1.1702
0.9201 1.2144	0.9401 1.2507
0.9600 1.2879	0.9800 1.3260
1.0000 1.3650
0 0.1000	0.0050 0.1050
0.0100 0.1100	0.0151 0.1151
0.0201 0.1201	0.0451 0.1451
0.0701 0.1701	0.0951 0.1951
0.1201 0.2202	0.1451 0.2453
0.1701 0.2705	0.1951 0.2957
0.2201 0.3210	0.2451 0.3465
0.2701 0.3721	0.2951 0.3978
0.3201 0.4238	0.3451 0.4499
0.3701 0.4764	0.3951 0.5031
0.4201 0.5301	0.4451 0.5576
0.4701 0.5854	0.4951 0.6137
0.5201 0.6425	0.5451 0.6718
0.5701 0.7017	0.5951 0.7323
0.6201 0.7636	0.6451 0.7956
0.6701 0.8285	0.6951 0.8622
0.7201 0.8968	0.7451 0.9325
0.7701 0.9691	0.7951 1.0069
0.8201 1.0459	0.8451 1.0860
0.8701 1.1275	0.8951 1.1702
0.9201 1.2144	0.9401 1.2507
0.9600 1.2879	0.9800 1.3260
1.0000 1.3650
0 0.1000	0.0050 0.1050
0.0100 0.1100	0.0151 0.1151
0.0201 0.1201	0.0451 0.1451
0.0701 0.1701	0.0951 0.1951
0.1201 0.2202	0.1451 0.2453
0.1701 0.2705	0.1951 0.2957
0.2201 0.3210	0.2451 0.3465
0.2701 0.3721	0.2951 0.3978
0.3201 0.4238	0.3451 0.4499
0.3701 0.4764	0.3951 0.5031
0.4201 0.5301	0.4451 0.5576
0.4701 0.5854	0.4951 0.6137

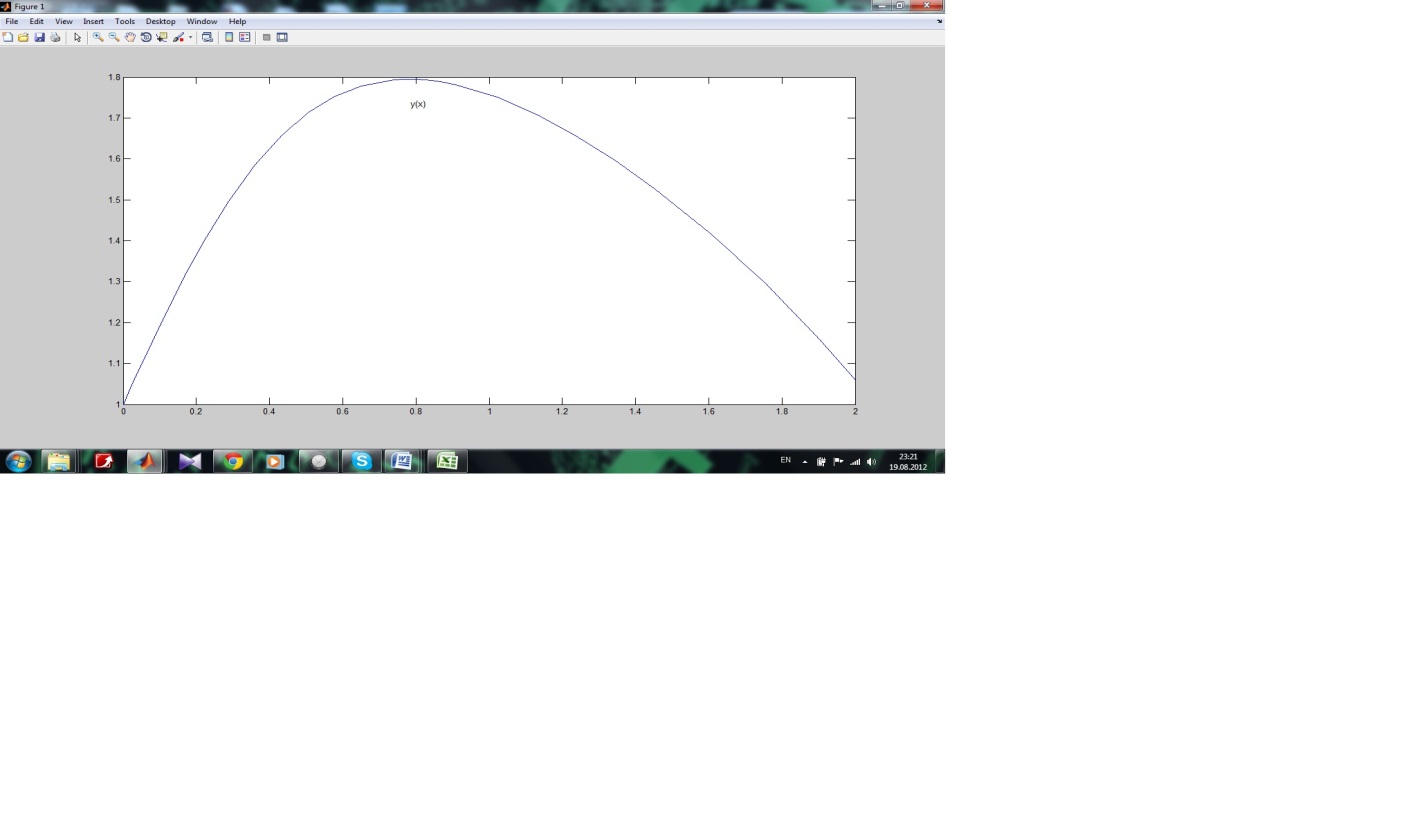
>>plot(X,Y)

>> hold on;gtext(' y(x) ')

>>plot(X,Y),grid

Побудова графіка чисельного рішеннязадачі Коші:

Висновок: На прикладі даного завдання, я обчислювала диференціальні рівняння з допомогою Matlab.

Завдання 1.5.

Завдання 5. Рівняння Ван-дер-Поля, що описує коливання в нелінійній системі (наприклад, автогенераторі), має наступний вигляд:

де у, у' і у" - функція, її перша і друга похідні за часом t. Постійна b визначає втрати в системі. Нелінійні властивості системи, наприклад, робочі характеристики активного елементу генератора, враховуються складовоюу .

Задавшись вказаними в таблиці початковими умовами і параметром b, розв’яжіть рівняння і побудуйте графіки залежностей у(t) і у'(f), що охоплюють декілька періодів коливань.

Параметр	Варіант
	36	37	38	39	40	41	42	43	44
у(0)	1	0	1	2	2	-3	-1	-2	1,5
у'(0)	1	1	-2	1	3	20	10	5	4
b	7	3y	y	y’	1.5y’	0	2y	2y’	5

%Запис в м-файлі

functiondy = vdp1(t,y)

dy = zeros(2,1); % a columnvector

dy(2) = y(1);

dy(1) = (y(1)-y(2)^2)*y(1)-y(2);

%в матлабі

>> [t,Y] = ode15s(@vdp1,[0 2],[1 2]);

>>plot(t,Y(:,1),'0')

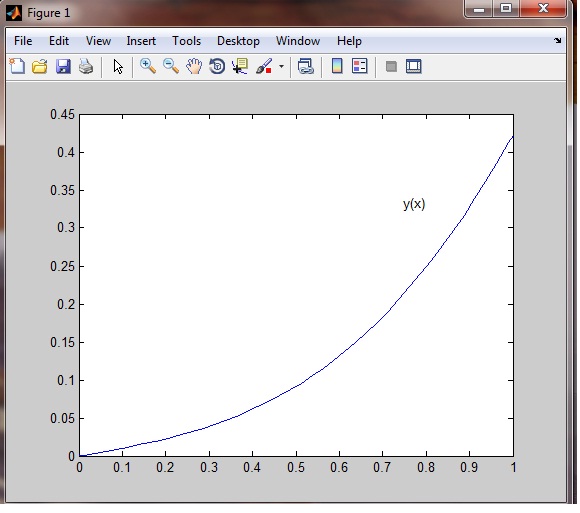
Висновок: Виконуючи дане завдання, ми промоделювали проходження електричних сигналів, розрахували і побудували графік залежності i(t).